1. От регрессии к нейросетке

Однажды вечером, по пути с работы, Маша зашла в свою любимую кофейню на Тверской. Там, на стене, она обнаружила интересную картину:

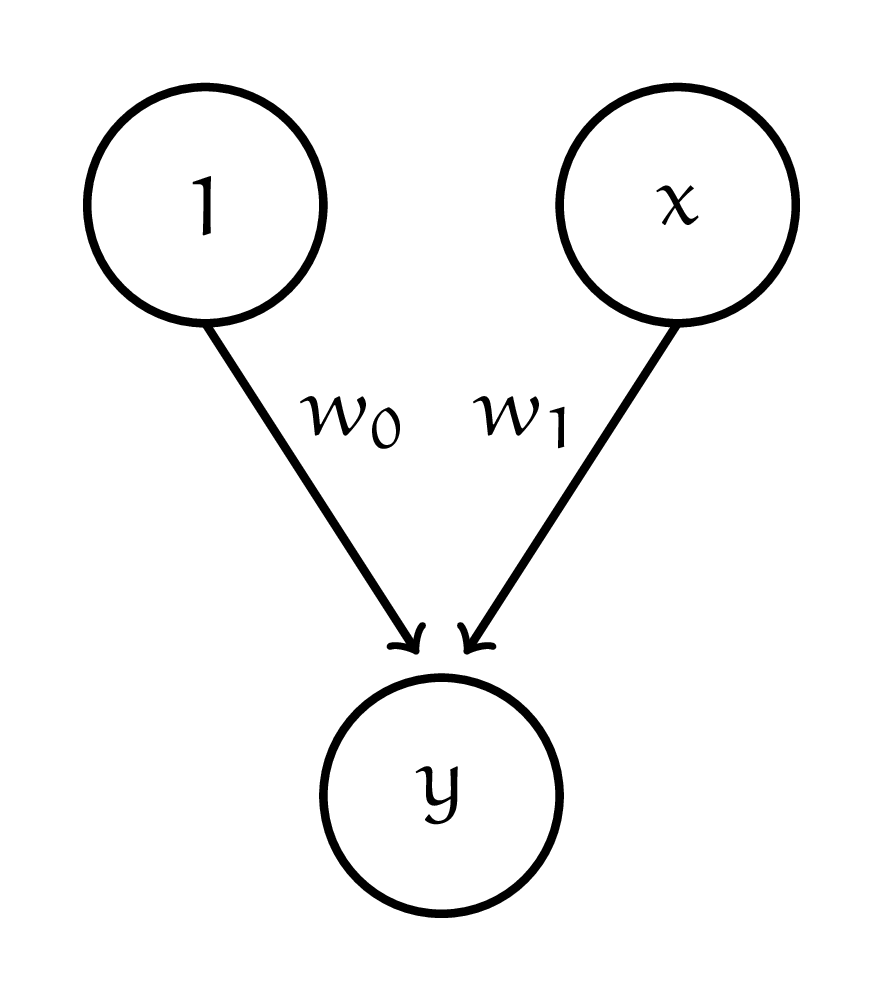
Хозяин кофейни, Добродум, объяснил Маше, что это Покрас-Лампас нарисовал линейную регрессию, и её легко можно переписать в виде формулы: \(y_i = w_0 + w_1 \cdot x_i.\) Пока Добродум готовил кофе, Маша накидала у себя на бумажке новую картинку:

Как такая функция будет выглядеть в виде формулы? Правда ли, что переменная \(y\) будет нелинейно зависеть от переменной \(x\)? Если нет, как это исправить и сделать зависимость нелинейной?

Решение

Когда Добродум записывал картинку в виде уравнения, он брал вход из кругляшей, умножал его на веса, написанные около стрелок и искал сумму. Сделаем ровно то же самое для Машиной картинки. Величины \(h_i\) внутри кругляшей скрытого слоя будут считаться как:

\[\begin{equation*} \begin{aligned} & h_1 = w_{11} \cdot 1 + w_{21} \cdot x \\ & h_2 = w_{12} \cdot 1 + w_{22} \cdot x \\ \end{aligned} \end{equation*}\]

Итоговый \(y\) будет получаться из этих промежуточных величин как

\[ y = w_1 \cdot h_1 + w_2 \cdot h_2. \]

Подставим вместо \(h_i\) их выражение через \(x\) и получим уравнение, которое описывает картинку Маши

\[\begin{multline*} y = w_1 \cdot h_1 + w_2 \cdot h_2 = \\ = w_1 \cdot (w_{11} + w_{21} \cdot x) + w_2 \cdot (w_{12} + w_{22} \cdot x) = \\ = \underbrace{(w_1 w_{11} + w_2 w_{12})}_{\gamma_1} + \underbrace{(w_1 w_{21} + w_2 w_{22})}_{\gamma_2} \cdot x. \end{multline*}\]

Когда мы раскрыли скобки, мы получили ровно ту же самую линейную регрессию. Правда мы зачем-то записали переменные \(\gamma_1\) и \(\gamma_2\) через шесть параметров. Чтобы сделать зависимость нелинейной, нужно преобразить каждую из \(h_i\), взяв от них нелинейную функцию. Например, сигмоиду

\[ f(h) = \frac{1}{1 + e^{-h}}. \]

Тогда формула изменится

\[ y = w_1 \cdot f(w_{11} + w_{21} \cdot x) + w_2 \cdot f(w_{12} + w_{22} \cdot x). \]

Линейности больше нет. Только что, на ваших глазах, произошло чудо. Регрессия превратилась в нейросеть. Функцию \(f(h)\) называют функцией активации. Вместо сигмоиды можно использовать другие функции. В современных нейросетях довольно часто используют ReLU (Rectified Linear Unit). Она нелинейная и просто вычисляется

\[ ReLU(h) = \max(0, h). \]

У такой функции активации много других прятных свойств. Мы их обсудим более подробно в четвёртом листочке.