1. Сигмоида

Сигмоида – это классическая функция активации. У неё есть куча проблем, из-за которых её нужно очень аккуратно использовать в глубоких нейронных сетях. Давайте обсудим эти проблемы и поймём, как правильно её использовать.

Любую \(s\)-образную функцию называют сигмоидой. Наиболее сильно прославилась под таким названием функция

\[ \sigma(t) = \frac{e^t}{1 + e^t} = \frac{1}{1 + e^{-t}}. \]

Слава о ней добралась до Маши и теперь она хочет немного поисследовать её свойства.[1]

а) Что происходит при \(t \to +\infty\)? А при \(t \to -\infty\)?

Решение

Мы знаем, что при \(t \to +\infty\) функция \(e^{-t} \to 0\), значит \(\sigma(t) \to 1.\)

По аналогии при \(t \to -\infty\) функция \(e^{-t} \to \infty\), значит \(\sigma(t) \to 0.\)

Сигмоида – это функция распределения логистической случайной величины. Обычно её используют при решении задачи классификации, чтобы отнормировать выход нейросети на отрезок \([0;1]\).

Если для оптимизации используется logloss, сигмоида интерпретируется как \(\mathbb{P}(y = 1 \mid x).\) Это можно формально доказать. В конспекте по МО-1 с ФКН описывается подход для этого. Мы займёмся этим в последней задачке этого листочка.

б) Как связаны между собой \(\sigma(t)\) и \(\sigma(-t)\)?

Решение

\[ \sigma(-t) = \frac{1}{1 + e^t} = \frac{1 + e^t - e^t}{1 + e^t} = 1 - \sigma(t). \]

в) Как связаны между собой \(\sigma(t)\) и \(\sigma'(t)\)?

Решение

Мы уже решали этот пункт в листочке про обратное распространение ошибки. Воспроизведём логику из него

\[\begin{multline*} \sigma'(t) = \left(\frac{e^t}{1 + e^{t}} \right)' = \frac{e^t}{1 + e^{t}} - \frac{e^t}{(1 + e^{t})^2} \cdot e^t = \\ = \frac{e^t}{1 + e^{t}} \left(1 - \frac{e^t}{1 + e^{t}} \right) = \sigma(t)(1 - \sigma(t)). \end{multline*}\]

г) Найдите \(\sigma(0)\) и \(\sigma'(0)\).

Решение

Подставим ноль в получившиеся формулы

\[\begin{equation*} \begin{aligned} & \sigma(0) = \frac{1}{1 + e^{-0}} = 0.5 \\ & \sigma'(0) = \sigma(0) \cdot (1 - \sigma(0)) = 0.25 \\ \end{aligned} \end{equation*}\]

д) Найдите обратную функцию \(\sigma^{-1}(t)\)

Решение

\[\begin{equation*} \begin{aligned} & y = \frac{1}{1 + e^{-t}} \\ & e^{-t} = \frac{1}{y} - 1 = \frac{1 - y}{y} & t = \ln \frac{y}{1 - y} \end{aligned} \end{equation*}\]

Вспомним, что \(\sigma(t) = \mathbb{P}(y = 1 \mid x)\), значит

\[ \sigma^{-1}(t) = \ln \frac{\mathbb{P}(y = 1 \mid x)}{1 - \mathbb{P}(y = 1 \mid x)}. \]

Эту величину называют логит. Когда с помощью нейронных сетей решают задачу классификации, часто специфицируют модель так, чтобы она прогнозировала на последнем слое логит. Если взять от логита сигмоиду, мы получим \(\mathbb{P}(y = 1 \mid x).\)

Кстати говоря, модель градиентного бустинга для классификации, обычно, собирают так, чтобы она тоже прогнозировала на выходе логит.

е) Как связаны между собой \([\ln \sigma(t)]'\) и \(\sigma(-t)\)?

Решение

\[ [\ln \sigma(t)]'_t = \frac{1}{\sigma(t)} \cdot \sigma'(t) = \frac{1}{\sigma(t)} \cdot \sigma(t) \cdot (1 - \sigma(t)) = 1 - \sigma(t) = \sigma(-t). \]

ё) Постройте графики функций \(\sigma(t)\) и \(\sigma'(t)\).

Решение

Сигмоида выглядит как функция распределения. Она не убывает. У неё две асимптоты, \(0\) и \(1\). Она выглядит S-образно. Её производная выглядит как выпуклый холмик. Если хочется, можно по-честному взять от неё все производные и построить график функции, как это делалось на математическом анализе.

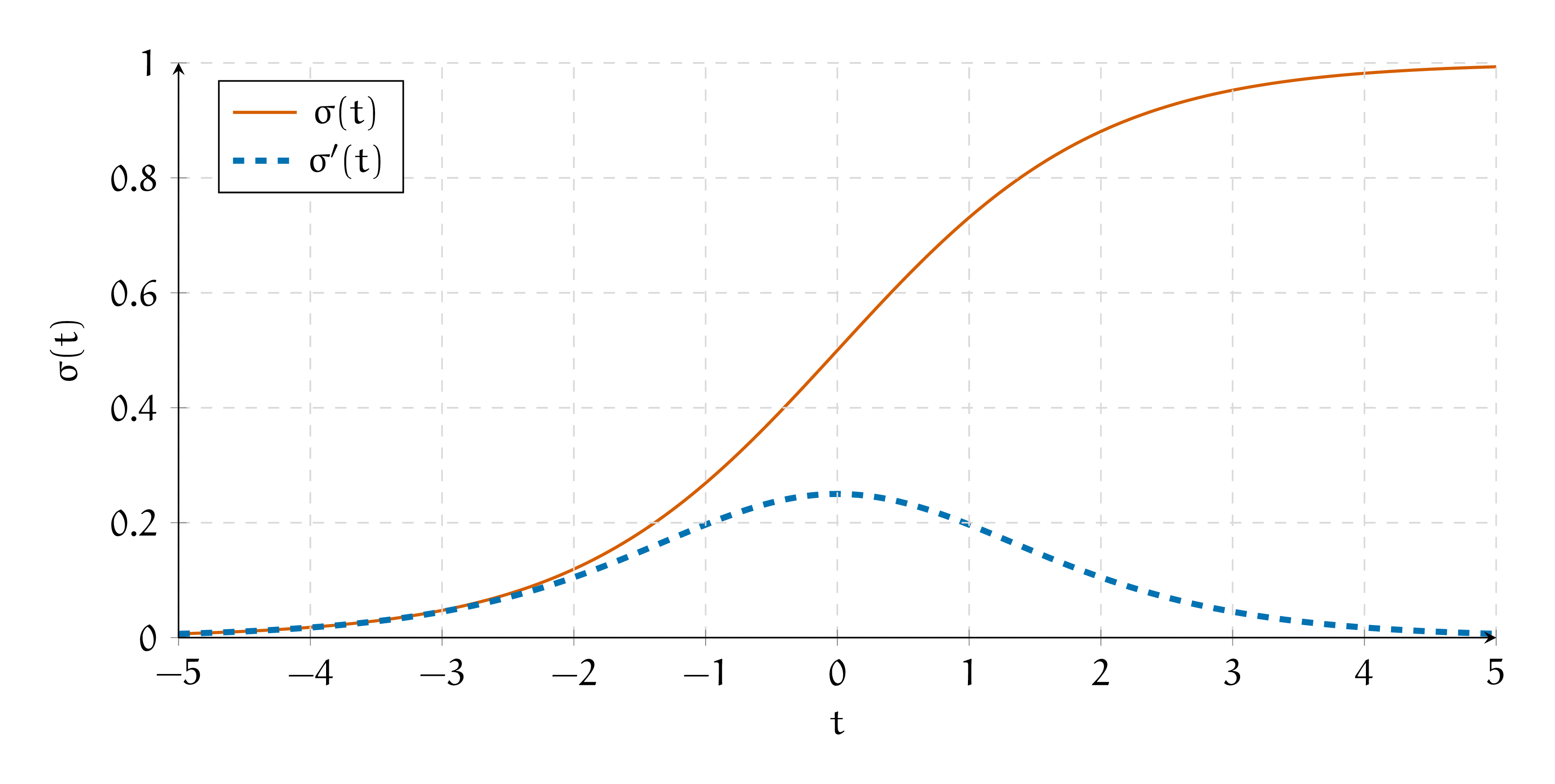
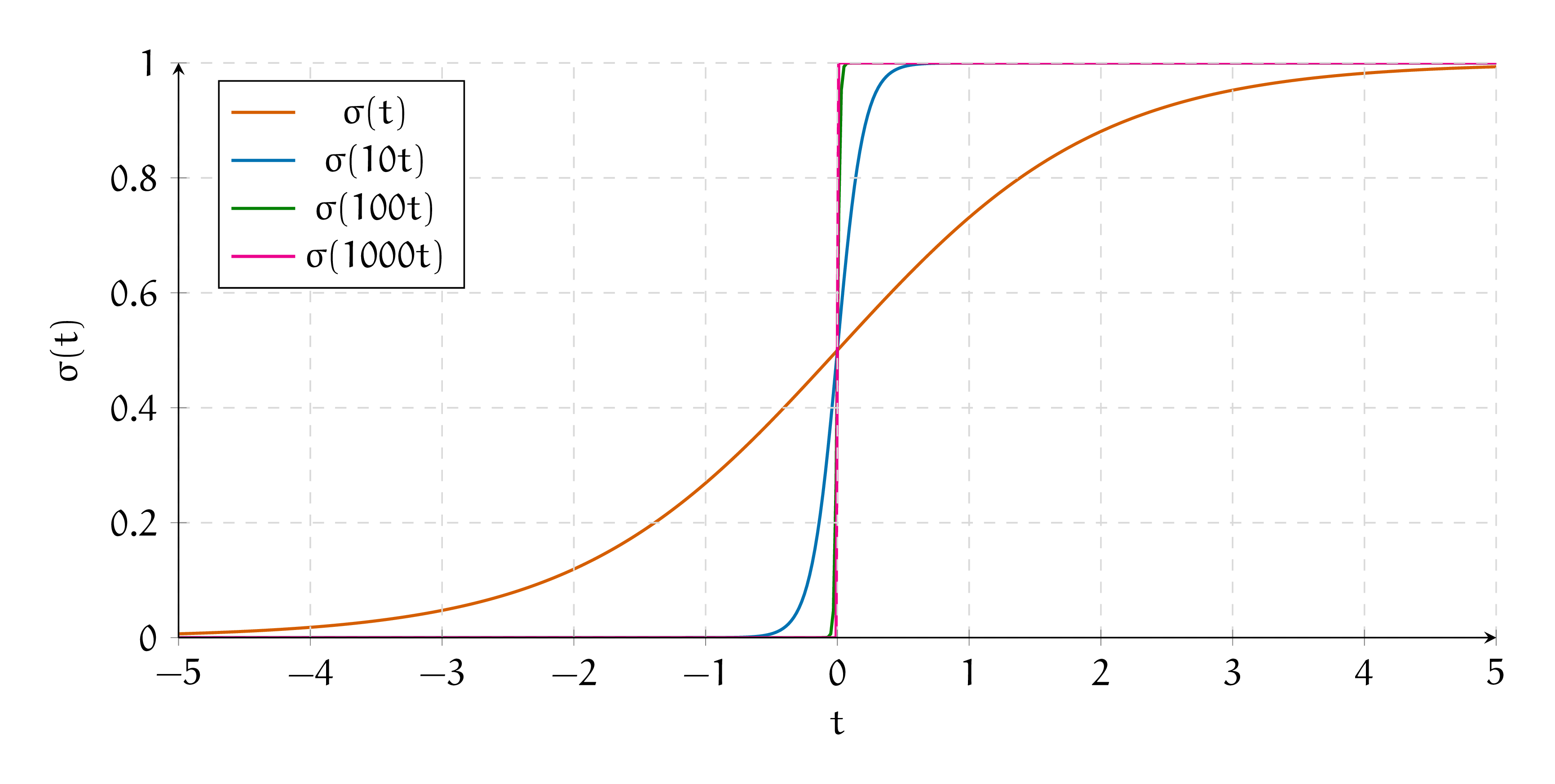
ж) Говорят, что сигмоида — это гладкий аналог единичной ступеньки. Попробуйте построить на компьютере графики \(\sigma(t), \sigma(10\cdot t), \sigma(100\cdot t), \sigma(1000\cdot t)\). Как они себя ведут?

Решение

Видно, что чем больше коэффициент перед \(t\), тем резче перепад у графика. При очень большом значении коэффициента, сигмоида очень напоминает ступеньку, но в отличие от неё она дифференцируема.

з) Выпишите формулы для forward pass и backward pass через слой с сигмоидой.

Решение

Мы уже нашли выше производную. У сигмоиды нет обучаемых параметров, получается прямой проход через неё делается по формуле

\[ o = \sigma(h). \]

Обратный шаг делается по формуле

\[ d = \sigma(h) \cdot (1 - \sigma(h)) \cdot d. \]

То же самое можно записать как

\[ \frac{\partial L}{\partial h} = \sigma(h) \cdot (1 - \sigma(h)) \cdot \frac{\partial L}{\partial o}. \]

и) Какое максимальное значение принимает производная сигмоиды? Объясните как это способствует затуханию градиента и параличу нейронной сети.

Решение

Проанализируем функцию

\[ f(\sigma) = \sigma \cdot (1 - \sigma) = \sigma - \sigma^2. \]

Это парабола. Её ветви смотрят вниз. Найдём её экстремум

\[ f'(\sigma) = 1 - 2\sigma = 0 \quad \Rightarrow \quad \sigma = 0.5 \]

Получается, что \(f(\sigma) \le 0.5 - 0.5^2 = 0.25\). Выходит, что производная сигмоиды принимает значение с отрезка \([0; 0.25].\) При шаге обратного распространения ошибки, мы умножаем уже накопившуюся производную на производную сигмоиды. Накопленная производная из-за этого уменьшается. Получается, что если нейросетка очень глубокая, до первых слоёв дойдёт очень маленькая производная. Веса будут двигаться на очень маленькие расстояния. Из-за этого обучение застопорится. Такая ситуация называется параличём нейронной сети либо проблемой затухания градиента (vanishing gradient problem).

Чтобы побороть проблему затухающих градиентов, надо модернизировать архитектуру нейронной сети так, чтобы не выскакивало затухающих производных. Из-за этого сигмоиду не используют в глубоких нейронных сетях и предпочитают ей другие функции активации.

Давайте ещё раз посмотрим на график сигмоиды и её производной.

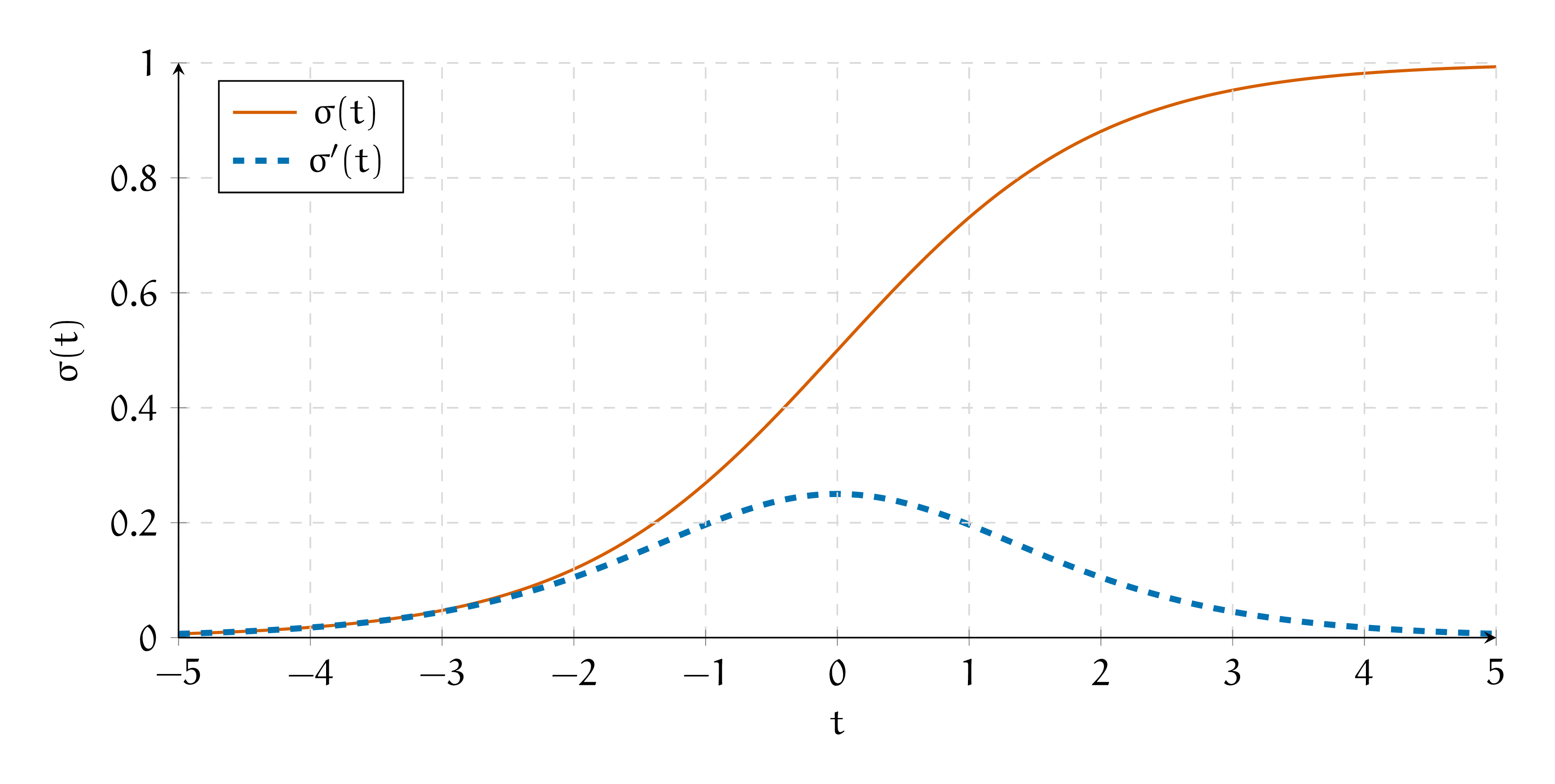
Каждый нейрон в нашей сетке либо активируется либо нет. Когда нейрон обучился, он выплёвывает значения близкие либо к единице либо к нулю. Производная на краях сигмоиды оказывается очень маленькой. Получается, что по мере обучения нейронной сети, проблема затухающих градиентов обостряется.

Ужаснее всего то, что на графике с функцией потерь всё выглядит так, будто обучение сошлось. Функция стабилизируется и прекращает убывать.

к) Сигмоида не центрированна относительно нуля. Из-за этого градиентный спуск работает плохо. Объясните, почему так происходит.

Решение

Мы находим выход слоя как \(o = \sigma(h)\). Он всегда положительный. Это означает, что все градиенты по весам линейного слоя, идущего перед сигмоидой будут либо положительными либо отрицательными (внимательно посмотрите на формулы из задачи 6 листочка про бэкпроп). Из-за этого веса будут всегда обновляться в одинаковом направлении.

Пусть у нас есть два параметра. По одному надо двигаться в положительную сторону, а по второму в отрицательную (голубая стрелка). Наши градиенты никогда не будут оказываться разных знаков. Они оба всегда будут либо положительными либо отрицательными. Из-за этого движение будет идти зиг-загами. В точку оптимума мы будем идти дольше.

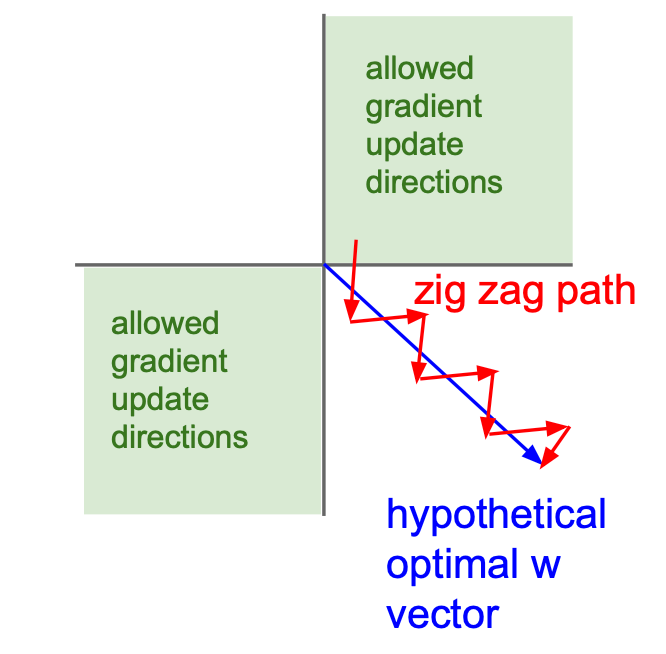
Чтобы избежать этого, нужно центрировать функцию активации относительно нуля. Тогда градиенты смогут принимать разные знаки и оптимизация будет работать быстрее.

Картинка взята из курса cs231n.

---

[1]

Задачка взята из коллекции Бориса Демешева и изменена до неузнаваемости.