Ctrl+K

1. Граф вычислений

1. Граф вычислений#

Как найти производную \(a\) по \(b\) в графе вычислений? Находим не посещённый путь из \(a\) в \(b\), перемножаем все производные на рёбрах получившегося пути. Добавляем это произведение в сумму. Так делаем для всех путей. Маша хочет попробовать этот алгоритм на функции

\[ f(x,y) = x^2 + xy + (x + y)^2. \]

Помогите ей нарисовать граф вычислений и найти \(\frac{\partial f}{\partial x}\) и \(\frac{\partial f}{\partial y}.\) В каждой вершине графа записывайте результат вычисления одной элементарной операции: сложений или умножения[1].

Решение

Нарисуем граф вычислений.

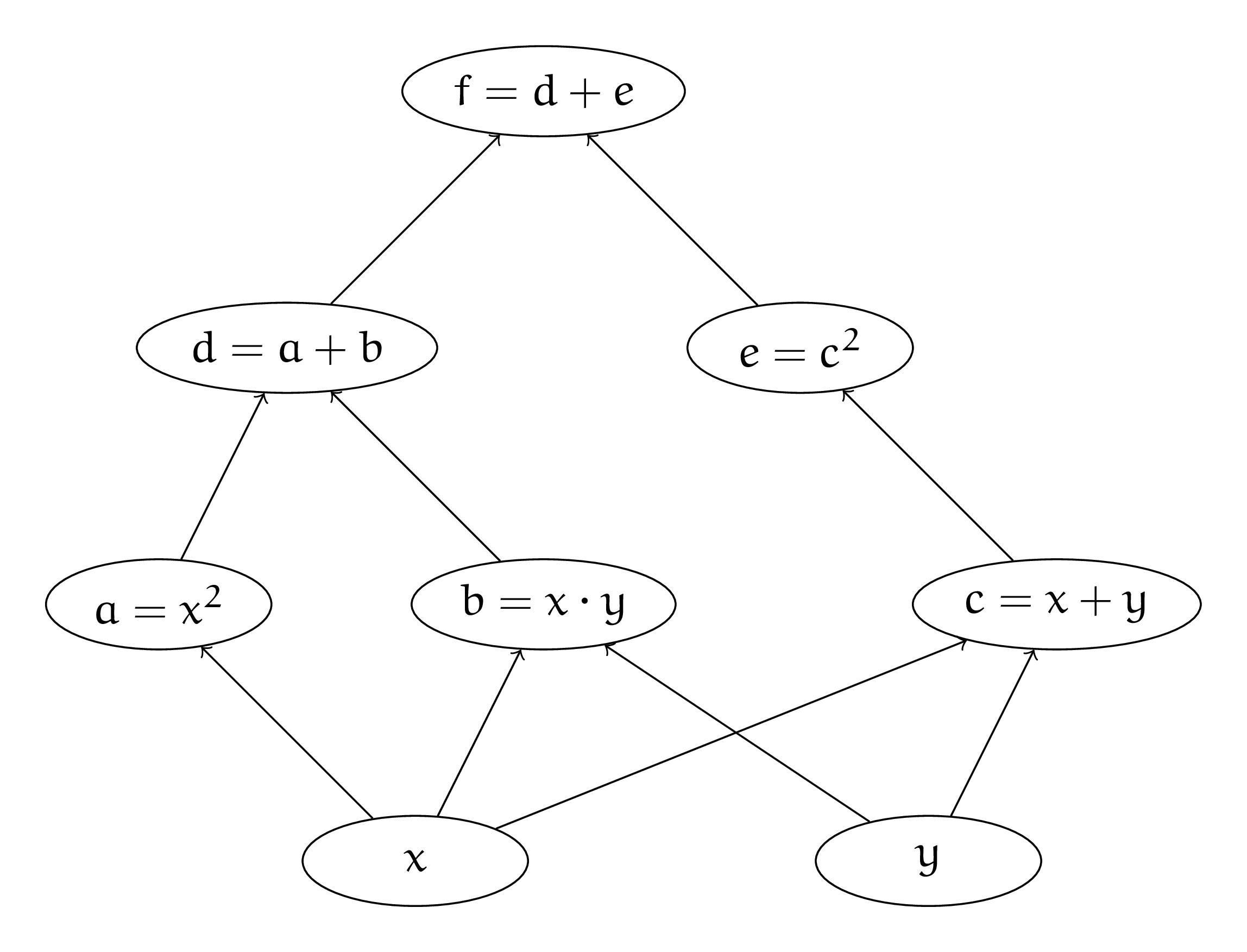
dobronet_forward

Каждому ребру припишем производную выхода по входу. Например, ребру между \(x\) и \(a\) будет соответствовать \(\frac{\partial a}{\partial x} = 2x.\)

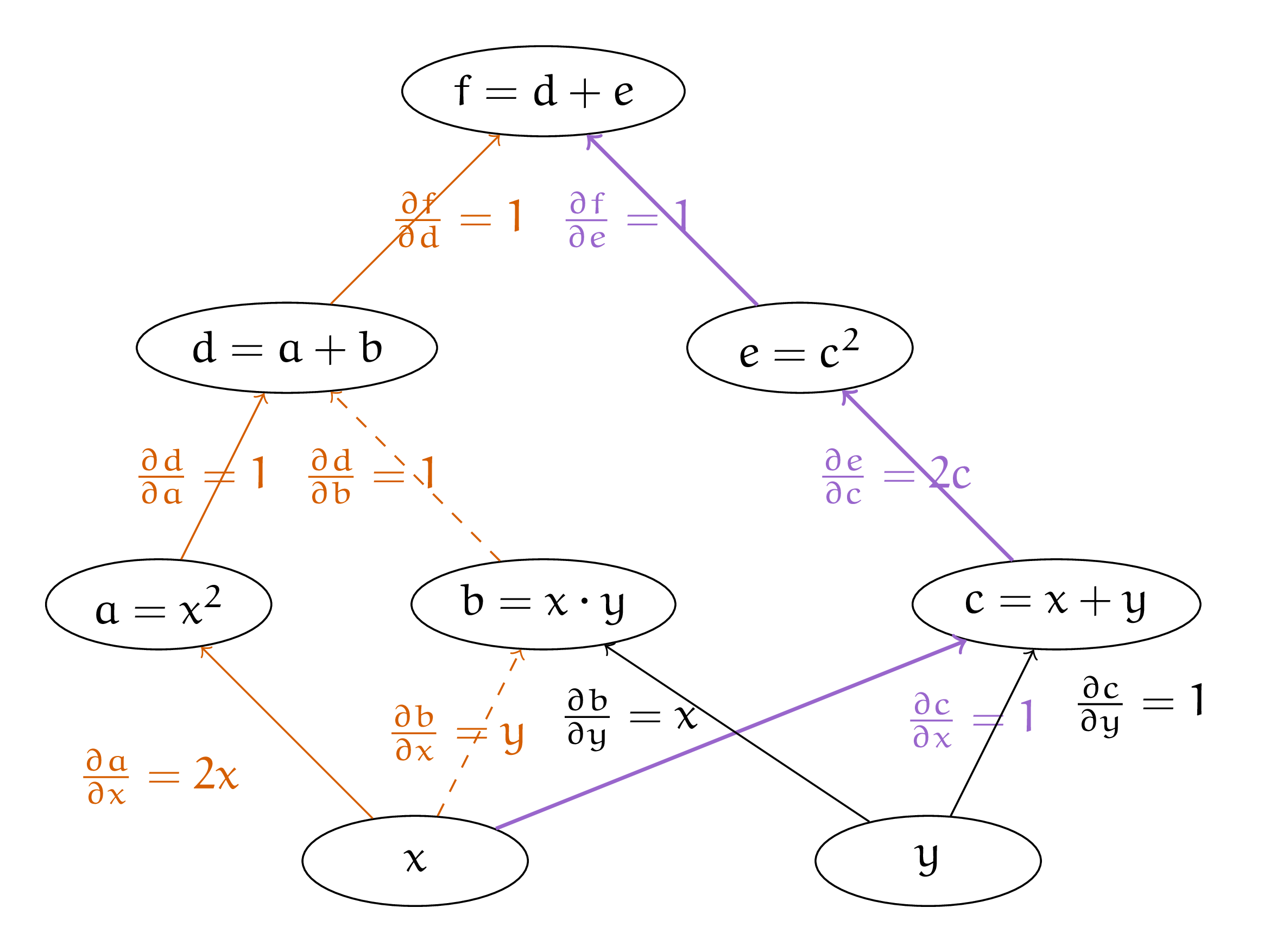
dobronet_forward

Теперь пройдём по всем траекториям из \(x\) в \(f\) и перемножим производные на рёбрах. После просуммируем получившиеся множители

\[\begin{multline*} \frac{\partial f}{\partial x} = \frac{\partial f}{\partial d} \cdot \frac{\partial d}{\partial a} \cdot \frac{\partial a}{\partial x} + \frac{\partial f}{\partial d} \cdot \frac{\partial d}{\partial b} \cdot \frac{\partial b}{\partial x} + \frac{\partial f}{\partial e} \cdot \frac{\partial e}{\partial c} \cdot \frac{\partial c}{\partial x} = \\ = 1 \cdot 1 \cdot 2x + 1 \cdot 1 \cdot y + 1 \cdot 2c \cdot 1 = 2x + y + 2(x + y). \end{multline*}\]

По аналогии найдём производную по траекториям из \(y\) в \(f\):

\[ \frac{\partial f}{\partial y} = 1 \cdot 1 \cdot x + 1 \cdot 2c \cdot 1 = x + 2(x + y). \]