Ctrl+K

2. Логистические потери и softmax

2. Логистические потери и softmax#

Маша решает задачу классификации. Она закодировала классы единичками и нулями. Логистическая функция потерь для одного наблюдения будет выглядеть как

\[ \text{logloss} = -(y_i \cdot \ln p_i + (1 - y_i) \cdot \ln (1 - p_i)). \]

Под \(p_i\) имеется в виду \(\mathbb{P}(y_i = 1 \mid x)\).

а) Нарисуйте логистические потери для \(y_i = 1\) и \(y_i = 0\) на графике. По оси абсцисс отложите \(p_i\), а по оси ординат значение функции потерь. Объясните, зачем от \(p_i\) нужно брать логарифм. Почему нельзя оптимизировать вместо logloss функцию

\[ -(y_i \cdot p_i + (1 - y_i) \cdot (1 - p_i))? \]
Решение

Если \(y_i = 1,\) от нашей функции потерь останется только первое слагаемое, \(-\ln p_i\). Если \(y_i = 0\), останется только второе слагаемое, \(-\ln (1 - p_i)\). Изобразим их на графике

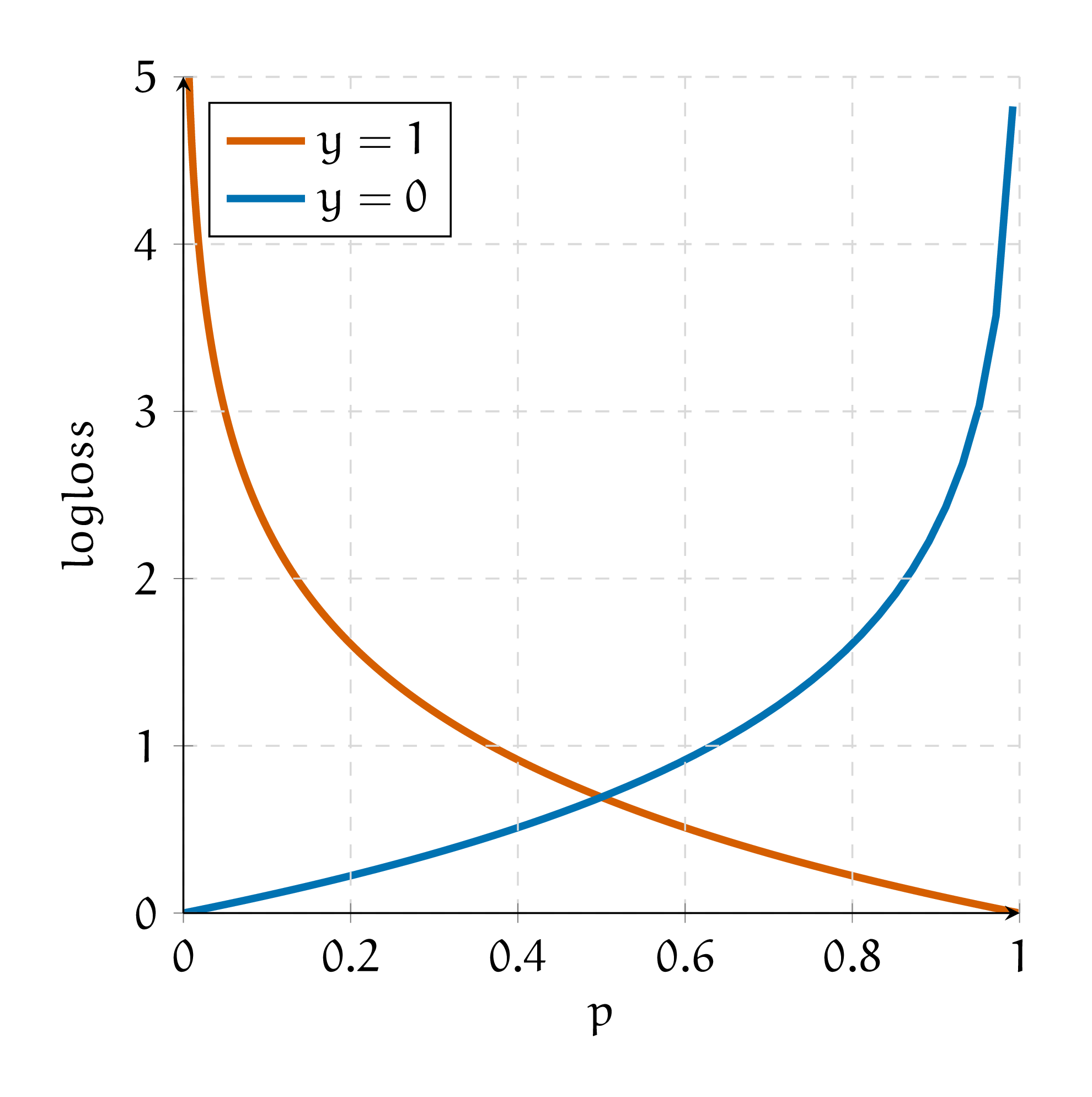
dobronet_forward

Если \(y_i = 1,\) мы хотим, чтобы \(p_i = \mathbb{P}(y_i = 1 \mid x)\) было как можно больше. Если \(p_i\) оказалась маленькой, штраф большой, если \(p_i\) оказалось большим, штраф будет маленьким. При этом, чем ближе \(p_i\) к единице, тем меньше мы его хотим увеличить. Такую нелинейность штрафа нам даёт логарифм. При \(y_i = 0\) логика точно такая же, но уже с \(\mathbb{P}(y_i = 0 \mid x)\).

Если мы сделаем штраф линейным, у такой функции потерь будет много проблем. Во-первых, пропадает нелинейность. Прирост ошибки в каждой точке одинаковый. Нам бы хотелось за мелкие ошибки штрафовать несерьёзно.

Во-вторых, из-за линейности такую функцию сложно оптимизировать. В-третьих, выхлоп модели нельзя будет интерпретировать как \(\mathbb{P}(y = 1 \mid x).\) Это можно формально доказать. Мы займёмся этим в последней задачке этого листочка.

У Маши три наблюдения, первое наблюдение — кит, остальные — муравьи. Киты кодируются как \(y_i = 1\), муравьи как \(y_i = 0\). В качестве регрессоров Маша берёт номера наблюдений \(x_i = i\). После этого Маша оценивает логистическую регрессию с константой. В качестве функции потерь используются логистические потери.[1]

б) Выпишите для данной задачи функцию потерь, которую минимизирует Маша.

Решение

Модель будет выглядеть как

\[\begin{equation*} \begin{aligned} & z_i = w_0 + w_1 x_i, \\ & p_i = \mathbb{P}(y_i = 1 \mid x) = \sigma(z_i) = \frac{1}{1 + e^{-(w_0 + w_1 x_i)}}. \end{aligned} \end{equation*}\]

Это обычная логистическая регрессия. Иначе говоря, это нейронная сеть, которая состоит из одного нейрона с сигмоидой в качестве функции активации.

Мы будем опимизировать логистические потери, то есть

\[ \text{logloss} = -\frac{1}{n} \sum_{i=1}^n \left( y_i \cdot \ln p_i + (1 - y_i) \cdot \ln (1 - p_i) \right). \]

Подставим наблюдения и получим

\[\begin{multline*} \text{logloss} = -\frac{1}{3} \cdot (\ln p_1 + \ln(1 - p_2) + \ln(1 - p_3)) = \\ = -\frac{1}{3} \cdot \left( \ln\sigma(w_0 + w_1) + \ln \sigma(-(w_0 + 2 \cdot w_1)) + \ln \sigma(-(w_0 + 3 \cdot w_1)) \right). \end{multline*}\]

Мы воспользовались тем, что \(\sigma(-t) = 1 - \sigma(t).\)

в) При каких оценках коэффициентов логистической регрессии эта функция достигает своего минимума?

Hint: Изобразите наблюдения на числовой прямой и подумайте как должна будет вести себя идеальная сигмоида. Обратите внимание, что выборка линейно-разделима.

Решение

Тут нужна картинка неописуемой красоты!

г) Маша чуть внимательнее присмотрелась к своему третьему наблюдению и поняла, что это не муравей, а бобёр. Теперь ей нужно решать задачу классификации на три класса. Как надо специфицировать выход из нейронной сетки и функцию потерь?

Решение

В случае бинарной классификации нейросеть выплёвывает один выход. К нему мы применяем сигмоиду и получаем вероятность первого класса. Если нам хочется получить вероятность нулевого класса, достаточно вычесть получившуюся вероятность из единицы.

Когда у нас появляется третий класс, одного выхода недостаточно. Обычно на последнем слое нейросети выставляют число нейронов, равное числу классов, а после применяют функцию softmax

\[\begin{equation*} \begin{aligned} (w_1^T x, &\ldots, w_K^Tx) \\ &\Downarrow \\ (e^{z_1}, &\ldots, e^{z_K}) \\ &\Downarrow \\ \left(\frac{e^{z_1}}{\sum_{k=1}^K e^{z_k}}\right., &\ldots,\left. \frac{e^{z_K}}{\sum_{k=1}^K e^{z_k}} \right) \end{aligned} \end{equation*}\]

Тогда мы получаем \(K\) выходов, лежащих на отрезке \([0;1]\). Они интерпретируются как уверенность нейросети в каждом из классов. В сумме эти выходы дают единицу.

dobronet_forward

Логистические потери для \(K\) классов можно записать как

\[ \text{logloss} = - \frac{1}{n} \sum_{i=1}^n \sum_{k=1}^K [y_i = k] \cdot \ln \frac{e^{w_k^Tx_i}}{\sum_{j=1}^{K} e^{w_j^Tx_i}}. \]

Здесь \([y_i = k]\) принимает значение равное единице, когда \(y_i = k,\) в остальных случаях это ноль.

Иногда числа, которые выплёвывает softmax слой интерпретируют как вероятность. Так можно делать не всегда. Выход нейросети всегда можно откалибровать так, чтобы он стал вероятностью.

В задаче классификации откалиброванным алгоритмом называют такой алгоритм, для которого доля положительных примеров (на основе реальных меток классов) для предсказаний в окрестности произвольной вероятности \(p\) совпадает с этим значением \(p\). Например, если взять объекты, для которых предсказанные вероятности близки к 0.7, то окажется, что среди них 70% принадлежат положительному классу.

Подробнее про калибровку алгоритмов можно почитать в конспекте по МО-1 с ФКН.

д) Маша уже обучила нейронную сетку и хочет построить прогнозы для двух наблюдений. Слой, который находится перед softmax выдал для этих двух наблюдений следующий результат: \((1, -2, 0)\) и \((0.5, -1, 0)\).

Чему равны вероятности получить кита, муравья и бобра для этих двух наблюдений?

Решение

Применим softmax к первому наблюдению

\[ \left( \frac{e^{1}}{e^{1} + e^{-2} + e^{0}}, \frac{e^{-2}}{e^{1} + e^{-2} + e^{0}}, \frac{e^{0}}{e^{1} + e^{-2} + e^{0}} \right) \approx (0.7, 0.03, 0.27). \]

По аналогии

\[ \left( \frac{e^{0.5}}{e^{0.5} + e^{-1} + e^{0}}, \frac{e^{-1}}{e^{0.5} + e^{-1} + e^{0}}, \frac{e^{0}}{e^{0.5} + e^{-1} + e^{0}} \right) \approx (0.55, 0.12, 0.33). \]

е) Пусть первым был кит, а вторым бобёр. Чему будет равна logloss-ошибка?

Решение

Кит на первой позиции, бобёр на последней. Значит logloss примет значение

\[ -\frac{1}{2} \cdot \left(\ln 0.7 + \ln 0.33 \right). \]

ё) Буква ё важна. Об этом вам скажут Лёв Толстой и Пафнутий Чебышёв. Объясните, почему softmax считают сглаженным вариантом arg max.

Решение

Softmax пытается заострить, преувеличить разницу между полученными значениями. Она выдаёт значения близкие к нулю для всех \(z_j,\) которые существенно меньше максимального. При этом softmax, в отличие от arg max, дифференцируема.

ж) Пусть у Маши есть два класса. Она хочет выучить нейросеть. Она может учить нейронку с одним выходом и сигмоидой в качестве функции активации либо нейронку с двумя выходами и softmax в качестве функции активации. Как выходы этих двух нейронок взаимосвязаны между собой?

Решение

Если мы учим нейросетку с одним выходом и сигмоидой, мы получаем на выходе

\[ \sigma(z) = \frac{1}{1 + e^{-z}} = \frac{e^{z}}{1 + e^z}. \]

Если у нас есть два выхода и мы применяем к ним softmax, мы получим

\[ \left( \frac{e^{z_1}}{e^{z_1} + e^{z_2}}, \frac{e^{z_2}}{e^{z_1} + e^{z_2}} \right). \]

Чтобы из второго элемента вектора получить сигмоиду, надо положить \(z_1 = 0, z_2 = z\). Посмотрим, что в таком случае будет происходить с первым элементом

\[ \frac{e^{z_1}}{e^{z_1} + e^{z_2}} = \frac{1}{1 + e^{z}} = \sigma(-z) = 1 - \sigma(z). \]

Получилось, что первый элемент представляет из себя вероятность того, что сетка выплюнула нулевой класс.

з) Докажите, что \(\text{softmax}(z + c) = \text{softmax}(z)\), где \(c\) — какая-то константа, прибавленная ко всем выходам слоя. Как этот факт позволяет сделать \(\text{softmax}\) численно устойчивой функцией и упростить для компьютера оптимизацию нейросети?

Решение

При поиске softmax мы ищем экспоненты, в памяти компьютера может произойти переполнение из-за больших чисел. Возникнут бесконечности и оптимизация нейронной сетки умрёт.

Если добавить ко всем входам нейронки одинаковую константу, значение sofrmax не изменится

\[ \frac{e^{z_i + c}}{\sum_{k=1}^K e^{z_k + c}} = \frac{ e^c \cdot e^{z_i } }{e^c \cdot \sum_{k=1}^K e^{z_k} } = \frac{e^{z_i}}{\sum_{k=1}^K e^{z_k }}. \]

Из-за этого, в нейросетях считают устойчивый к переполнению softmax

\[ \text{softmax}(z_1, \ldots, z_{K}) = \text{softmax}(z_1 - \max_i (z_i), \ldots, z_{K} - \max_i (z_i)). \]

и) Предположим, что на последнем слое найшей нейросети мы используем softmax. В качестве функции потерь мы используем \(\text{logloss}\). Как будет Выглядеть производная \(\frac{\partial \text{logloss}}{\partial z}\)?

Решение

Нам надо найти производную \(\frac{\partial \text{logloss}}{\partial z} = \frac{\partial \text{logloss}}{\partial p} \cdot \frac{\partial p}{\partial z}.\) Будем рассуждать в терминах одного наблюдения. Начнём с softmax

\[ p_i = \frac{e^{z_i}}{\sum_{k=1}^K e^{z_k}}. \]

На вход в softmax идет \(k\) элементов, на выходе получается \(k\) элементов. Нам надо взять производную каждого по каждому. Получается, что производная softmax – это матрица размера \(k \times k.\) У нас будет две ситуации: \(i = j\) и \(i \ne j\). Начнёмс с \(i = j\)

\[\begin{align*} \frac{\partial p_i}{\partial z_j} = \frac{\partial \frac{e^{z_i}}{\sum_{k=1}^K e^{z_k}}}{\partial z_j}&= \frac{e^{z_i} \sum_{k=1}^K e^{z_k} - e^{z_j}e^{z_i}}{\left( \sum_{k=1}^K e^{z_k}\right)^2} \\ &= \frac{e^{z_i} \left( \sum_{k=1}^K e^{z_k} - e^{z_j}\right )}{\left( \sum_{k=1}^K e^{z_k}\right)^2} \\ &= \frac{ e^{z_j} }{\sum_{k=1}^K e^{z_k} } \cdot \frac{\left( \sum_{k=1}^K e^{z_k} - e^{z_j}\right ) }{\sum_{k=1}^K e^{z_k} } \\ &= p_i \cdot (1-p_j). \end{align*}\]

Продолжим случаем \(i \ne j\)

\[\begin{align*} \frac{\partial \frac{e^{z_i}}{\sum_{k=1}^K e^{z_k}}}{\partial z_j}&= \frac{0 - e^{z_j}e^{z_i}}{\left( \sum_{k=1}^K e^{z_k}\right)^2} \\ &= \frac{- e^{z_j} }{\sum_{k=1}^K e^{z_k} } \cdot \frac{e^{z_i} }{\sum_{k=1}^K e^{z_k} } \\ &= - p_j \cdot p_i. \end{align*}\]

Получается, что производная выглядит как

\[\begin{split} \frac{\partial p_i}{\partial z_j} = \begin{cases}p_i \cdot (1-p_j), & i = j \\ -p_j \cdot p_i, & i \ne j. \end{cases} \end{split}\]

Давайте для удобства перепишем метки классов в OHE виде. Если \(y_i = k,\) мы будем представлять его в виде вектора, где на \(k-\)ой позиции стоит единица. Остальные элементы будут нулевыми. В этом пункте везде под \(y_i\) мы будем иметь в виду такой вектор. Для одного наблюдения logloss можно записать как

\[ \text{logloss} = -\sum_{k=1}^K y_i \cdot \ln p_i. \]

Берём производную

\[\begin{align*} \frac{\partial L}{\partial z_j} &= - \sum_k y_k \frac{\partial \ln(p_k)}{\partial z_j } \\ &= - \sum_k y_k \frac{\partial \ln (p_k)}{\partial p_k} \cdot \frac{\partial p_k}{ \partial z_j} \\ &= - \sum_k y_k \frac{1}{p_k} \cdot \frac{\partial p_k}{\partial z_j}. \\ \end{align*}\]

Подставим в формулу производную softmax

\[\begin{align*} \frac{\partial L}{\partial z_j} &= -y_j \cdot (1 - p_j) - \sum_{k \ne j} y_k \frac{1}{p_k}(-p_k \cdot p_j) \\ &= -y_j \cdot (1 - p_j) + \sum_{k \ne j} y_k \cdot p_j \\ &= - y_j + y_j p_j + \sum_{k \ne j} y_k \cdot p_j \\ &= p_j \left( y_j + \sum_{k \ne j} y_k\right) - y_j \\ &= p_j \sum_{k = 1}^K y_k - y_j = p_j - y_j. \end{align*}\]

Функция \(\text{logloss}\) бьёт из векторов \(z\) в константы. Производной будет вектор размера \(K\). Ровно такой вектор у нас и получается, то есть \(p - y\).

Мы нашли производную для одного наблюдения. Когда наблюдений становится много, мы должны просуммировать все потери по ним. Производная суммы будет равна сумме производных.