4. Армия регрессий

Маша любит собирать персептроны и думать по вечерам об их весах и функциях активации. Сегодня она решила разобрать свои залежи из персептронов и как следует упорядочить их. [1]

а) В ящике стола Маша нашла перcептрон с картинки перый персептрон. Маша хочет подобрать веса так, чтобы он реализовывал логическое отрицание, то есть превращал \(x_1 = 0\) в \(y=1\), а \(x_1 = 1\) в \(y=0\).

Fig. 1 перый персептрон

Решение

Чтобы было легче, запишем нейрон в виде уравнения:

\[ \hat y = \max(0, w_1 + w_2 \cdot x_1). \]

Нам нужно, чтобы

\[\begin{equation*} \begin{aligned} \max(0, w_1 + w_2 \cdot 1) = 0 \\ \max(0, w_1 + w_2 \cdot 0) = 1 \end{aligned} \end{equation*}\]

На второе уравнение \(w_2\) никак не влияет, а \(w_1 = 1.\) Для того, чтобы в первом уравнении получить ноль, нужно взять любое \(w_2 \le -1\).

б) В тумбочке, среди носков, Маша нашла перcептрон, с картинки второй персептрон. Маша хочет подобрать такие веса \(w_i\), чтобы персептрон превращал \(x_1, x_2, x_3\) из таблички ниже в соответствующие \(y\):

\(x_1\)	\(x_2\)	\(x_3\)	\(y\)
\(1\)	\(1\)	\(2\)	\(0.5\)
\(1\)	\(-1\)	\(1\)	\(0\)

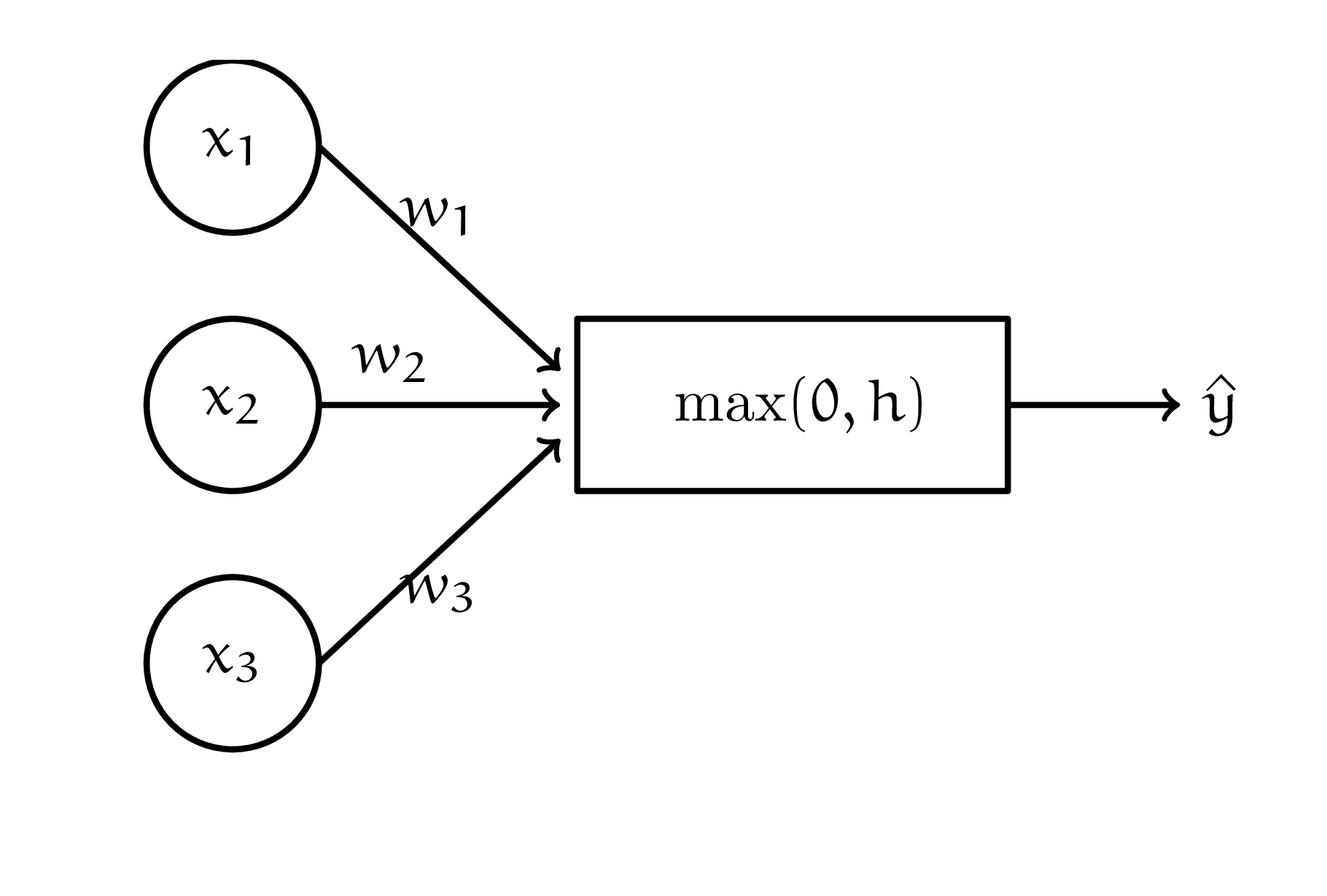
Fig. 2 второй персептрон

Решение

Снова выписываем несколько уравнений:

\[\begin{equation*} \begin{aligned} & \max(0, w_1 + w_2 + 2 \cdot w_3) = 0.5 \\ & \max(0, w_1 - w_2 + w_3) = 0 \end{aligned} \end{equation*}\]

Тут решений может быть довольно много. Одно из них — это занулить \(w_1\) и \(w_3\) в первом уравнении, а \(w_2\) поставить \(0.5\). Тогда во втором уравнении мы сразу же будем оказываться в отрицательной области и \(ReLU\) заботливо будет отдавать нам \(0\).

в) Оказывается, что в ванной всё это время валялась куча персептронов с картинки третий персептрон с неизвестной функцией активации.

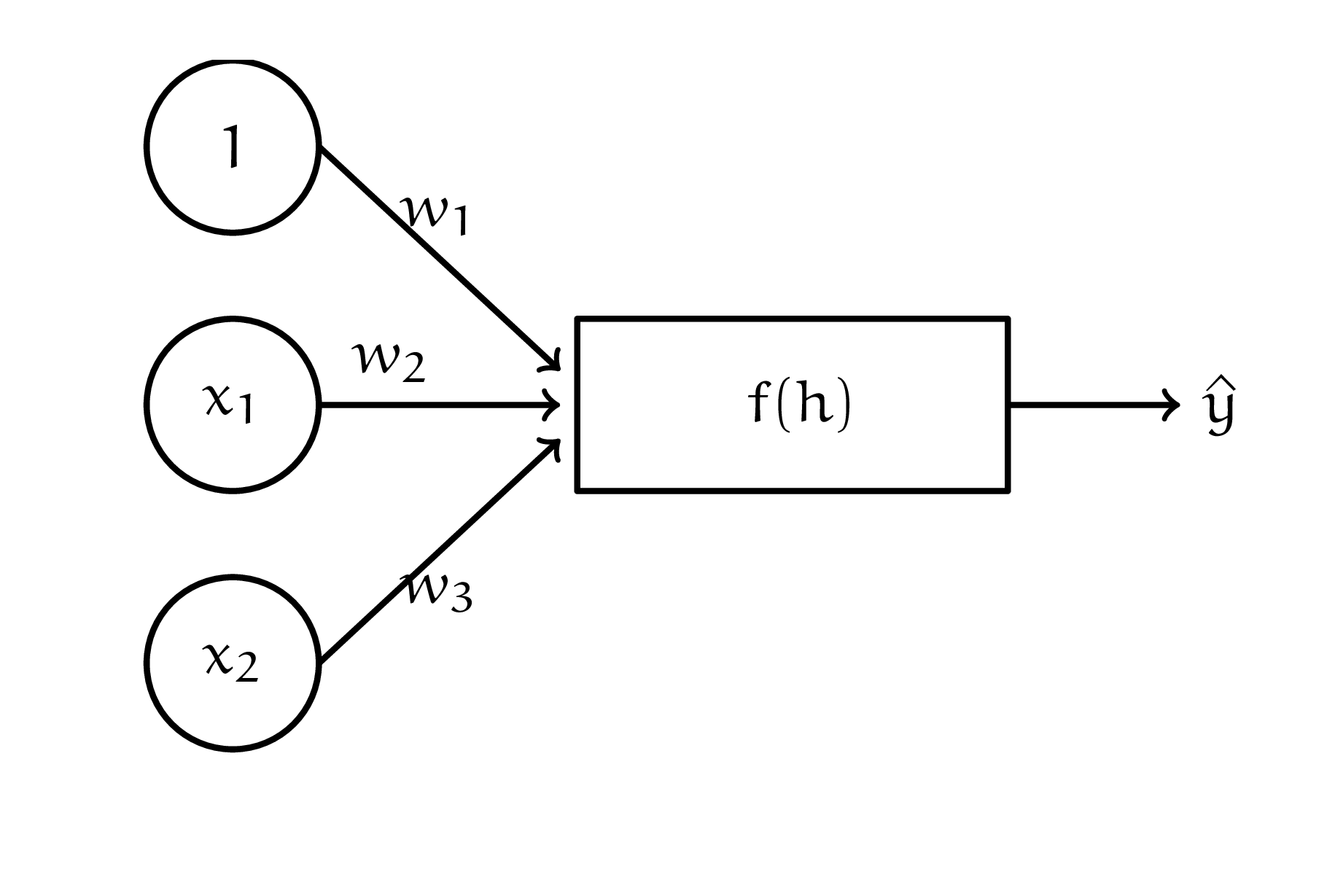
Fig. 3 третий персептрон

Маша провела на плоскости две прямые: \(x_1 + x_2 = 1\) и \(x_1 - x_2 = 1\). Она хочет собрать из персептронов нейросетку, которая будет классифицировать объекты с плоскости так, как показано на картинке данные. В качестве функции возьмите единичную ступеньку (Функцию Хевисайда)

\[\begin{split} f(h) = \begin{cases} 1, h > 0 \\ 0, h \le 0. \end{cases} \end{split}\]

Fig. 4 данные

Решение

Один нейрон — это одна линия, проведённая на плоскости. Эта линия отделяет один класс от другого. Например, линию \( x_1 + x_2 - 1 = 0 \) мог бы описать нейрон

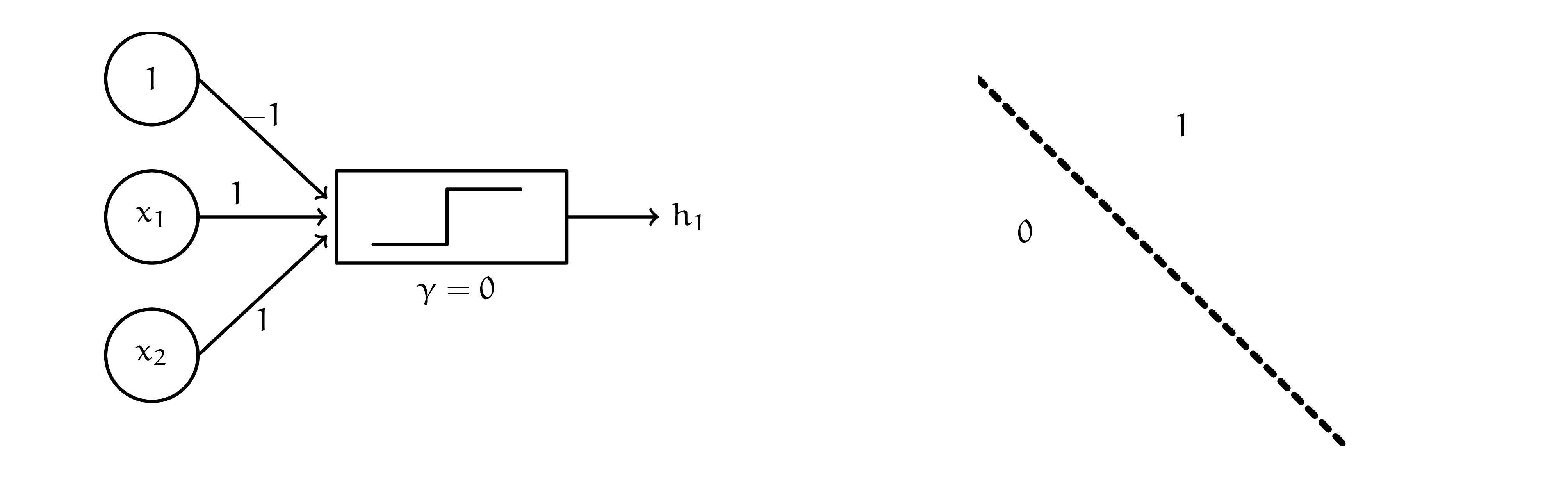
Порог \(\gamma\) для кусочной функции в каком-то смысле дублирует константу. Они взаимосвязаны. Будем всегда брать его нулевым. Видим, что если мы получили комбинацию \(x_1\), \(x_2\) и \(1\), большую, чем ноль, мы оказались справа от прямой. Если хочется поменять метки \(0\) и \(1\) местами, можно умножить все коэффициенты на \(-1\).

Наш персептрон понимает по какую сторону от прямой мы оказались, то есть задаёт одну линейную разделяющую поверхность. По аналогии для второй прямой мы можем получить следующий нейрон.

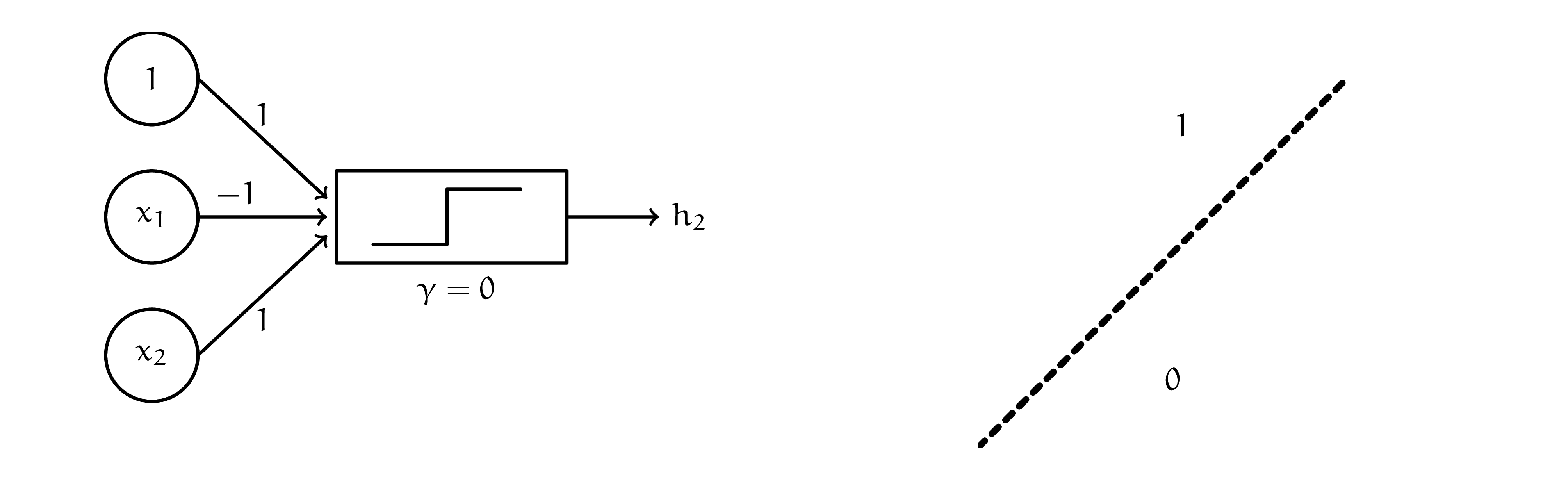
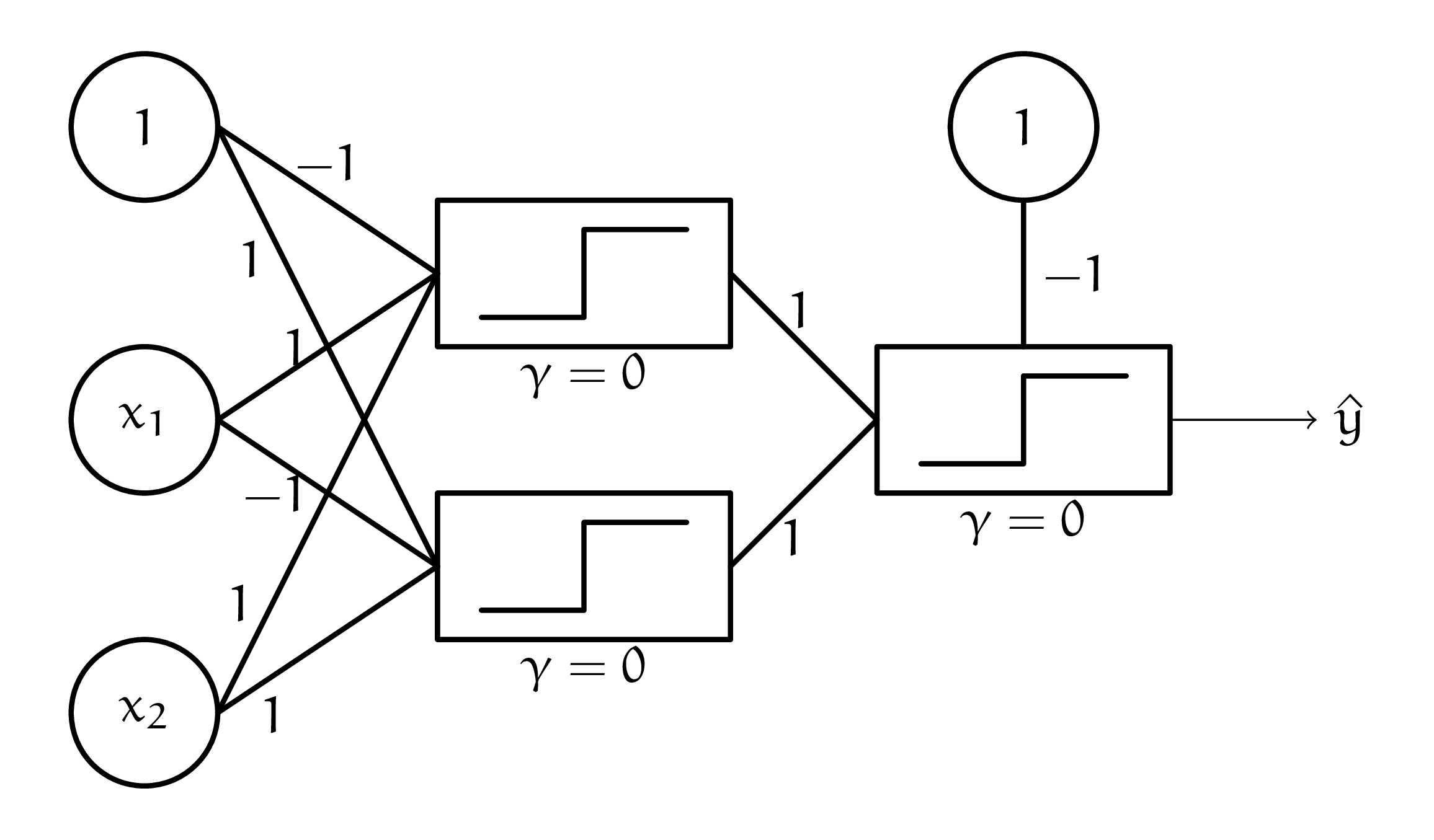
Итак, первый персептрон выбрал нам позицию относительно первой прямой, второй относительно второй. Остаётся только объединить эти результаты. Нейрон для скрепки должен реализовать для нас логическую функцию, которую задаёт табличка ниже. Там же нарисованы примеры весов, которые могли бы объединить выхлоп первого слоя в итоговый прогноз.

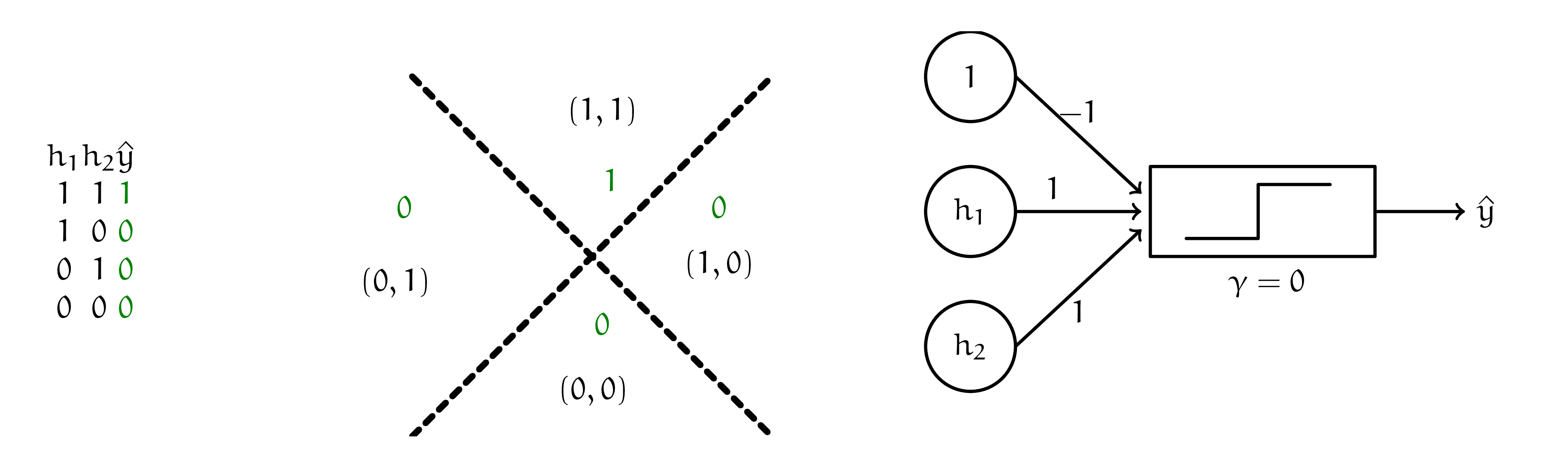
Теперь мы можем нарисовать итоговую нейронную сеть, решающую задачу Маши. Она состоит из двух слоёв. Меньше не выйдет, так как каждый персептрон строит только одну разделяющую линию.

Если бы мы ввели для нашей нейросетки дополнительный признак \(x_1 \cdot x_2\), у нас бы получилось обойтись только одним персептроном. В нашей ситуации нейросетка сама сварила на первом слое признак, которого ей не хватало для решения задачи. Другими словами говоря, нейросетка своим первым слоем превратила сложное пространство признаков в более простое, а затем вторым слоем, решила в нём задачу классификации.

---

[1]

Задачка взята из коллекции Бориса Демешева