5. Бэкпроп в матричном виде

У Маши есть нейросеть с картинки ниже, где \(w_{ij}^k\) — веса для \(k-\)го слоя, \(f(t)\) — какая-то функция активации. Маша хочет научиться делать для такой нейронной сетки градиентный спуск.

See also

Мы будем записывать все производные в матричном виде. Иногда будут всплывать слова «матричные производные». При разборе этой задачи можно про них ничего не знать, в решении они не используются. Мы нашли в предыдущих упражнениях все производные, нужные для вывода алгоритма обратного распространения ошибки. Тем не менее, техника матричного дифференцирования очень полезна. Поэтому я рекомендую вам её изучить. Ей посвящена последняя глава книги.

а) Запишите Машину нейросеть, как сложную функцию. Сначала в виде нескольких уравнений, а затем в матричном виде.

Решение

Договоримся до следующих обозначений. Буквами \(h^k_{ij}\) будем обозначать выход \(k-\)го слоя для \(j-\)го нейрона для \(i-\)го наблюдения до применения функции активации. Буквами \(o^k_{ij}\) будем обозначать всё то же самое после применения функции активации. Например, для первого слоя:

\[\begin{equation*} \begin{aligned} & h^1_{i1} = w^1_{11} \cdot x_{i1} + w^1_{21} \cdot x_{i2} \\ & o^1_{i1} = f(h_{i1}^1). \\ \end{aligned} \end{equation*}\]

Делай раз. Для начала перепишем сетку в виде нескольких уравнений. Для первого слоя мы находим

\[\begin{equation*} \begin{aligned} & o^1_{i1} = f( w^1_{11} \cdot x_{i1} + w^1_{21} \cdot x_{i2}) \\ & o^1_{i2} = f( w^1_{12} \cdot x_{i1} + w^1_{22} \cdot x_{i2}). \\ \end{aligned} \end{equation*}\]

Для второго работают аналогичные уравнения, но значения \(x\) заменяются на соответствующие \(o\). На выходе мы предсказываем \(y\), как взвешенную суммы выходов со второго слоя

\[ \hat{y}_i = w_1^3 \cdot o^2_{i1} + w_2^3 \cdot o^2_{i2}. \]

Подставим вместо \(o^2_{1i}\) и \(o^2_{2i}\) результат вычисления предыдущих слоёв

\[ \hat{y}_i = w_1^3 \cdot f( w^1_{12} \cdot o^1_{i1} + w^1_{22} \cdot o^1_{i2}) + w_2^3 \cdot f( w^1_{12} \cdot o^1_{i1} + w^1_{22} \cdot o^1_{i2}). \]

Подставим результат вычисления первого слоя

\[\begin{multline*} \hat{y}_i = w_1^3 \cdot f( w^1_{12} \cdot f( w^1_{11} \cdot x_{i1} + w^1_{21} \cdot x_{i2}) + w^1_{22} \cdot f( w^1_{12} \cdot x_{i1} + w^1_{22} \cdot x_{i2})) + \\ + w_2^3 \cdot f( w^1_{12} \cdot f( w^1_{11} \cdot x_{i1} + w^1_{21} \cdot x_{i2}) + w^1_{22} \cdot f( w^1_{12} \cdot x_{i1} + w^1_{22} \cdot x_{i2})). \end{multline*}\]

Мы записали нашу нейросеть в виде сложной функции. Выглядит ужасно.

Давайте перепишем всё то же самое более компактно, в матричном виде. Начнём с первого слоя. На самом деле, чтобы найти строчку \((h^1_{i1}, h^1_{i2})\) мы делаем матричное умножение. Строчку \((x_{i1}, x_{i2})\) мы умножаем на матрицу весов \(W_1\)

\[\begin{equation*} \begin{pmatrix} h^1_{i1} & h^1_{i2} \end{pmatrix} = \begin{pmatrix} x_{i1} & x_{i2}\end{pmatrix} \cdot \begin{pmatrix} w^1_{11} & w^1_{12} \\ w^1_{21} & w^1_{22}\end{pmatrix}. \end{equation*}\]

Чтобы получить \(h_1\) мы умножаем строчку из переменных на первый столбец, чтобы получить \(h_2\), на второй столбец. Получается, что в терминах матриц каждый нейрон нашей сети — это столбец. Если мы добавим ещё один столбец из весов в матрицу, это будет эквивалентно добавлению в сетку третьего нейрона, так как на выходе мы будем получать ещё и \(h_3\). Если у нас появится дополнительный вход \(x_3\), в матрицу нам нужно будет добавить ещё одну строчку из весов.

Запишем первый слой в матричном виде. На вход идёт матрица из наблюдений \(X_{[n \times 2]}\), она умножается на матрицу весов \(W_{[2 \times 2]}\), получается матрица \(H_{[n \times 2]}\). Ко всем элементам этой матрицы мы применяем функцию активации \(f\). Делаем это поэлементно

\[ O_1 = f(H_1) = f(X\cdot W_1). \]

Остальные слои записываются по аналогии. Получается, что наша нейросеть в матричном виде выглядит как

\[ \hat{y} = f(f(X\cdot W_1) \cdot W_2) \cdot W_3. \]

Здесь \(\hat{y}\) — вектор столбец размера \([n \times 1]\), а матрицы весов обладают размерностями \([2 \times 2]\), \([2 \times 2]\) и \([2 \times 1]\) соответственно.

б) Выпишите все производные в том виде, в котором их было бы удобно использовать для алгоритма обратного распространения ошибки, а затем, сформулируйте сам алгоритм. Нарисуйте под него удобную схемку.

Решение

Делай два. Выпишем алгоритм обратного распространения ошибки в виде красивой схемки. Сначала мы делаем прямой проход по нейросети (forward pass):

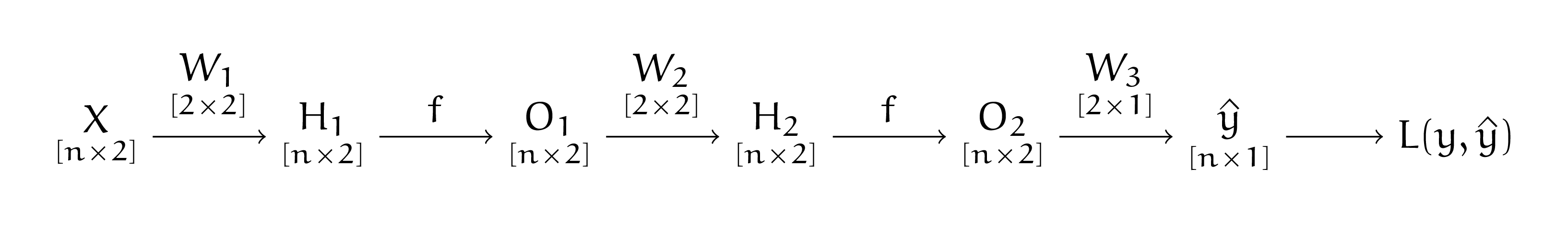
Под всеми матрицами подписаны размерности. Взятие функции активации — поэлементная операция, она никак не меняет размер матрицы. Это будет важно при взятии производных. В ходе прямого прохода мы запоминаем все промежуточные результаты. Они нам пригодятся для поиска производных при обратном проходе. Например, \(\frac{\partial H_2}{\partial W_2} = O_1^T.\) Получается, в какой-то момент нам надо будет переиспользовать результаты вычислений, полученных при прямом проходе.

Наша нейросеть — граф вычислений. Давайте запишем для каждого ребра в рамках этого графа производную.

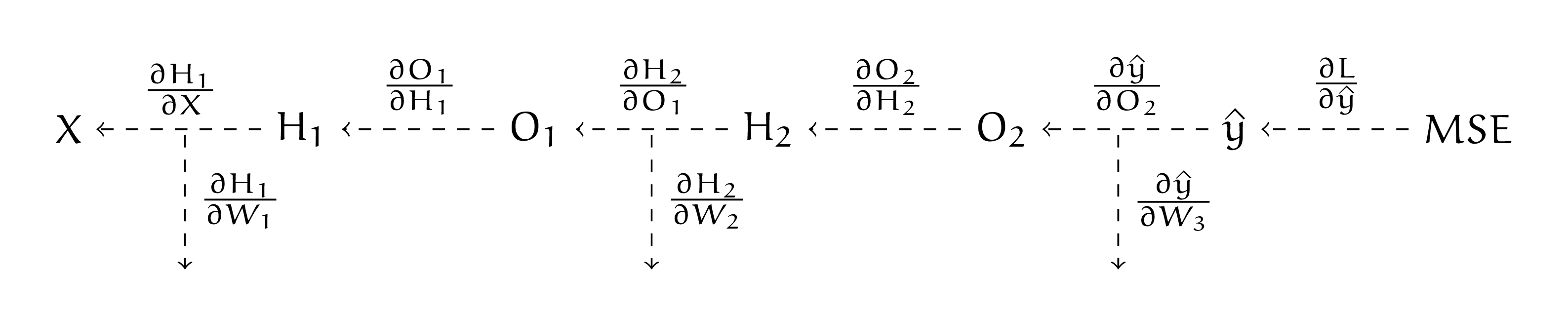
Осталось только аккуратно записать обратный ход алгоритма. Заведём для накопленного значения производной переменную \(d\). На первом шаге нам надо найти \(\frac{\partial L}{\partial W_3}\). Не будем забывать, как выглядят производные для линейного слоя, полученные в предыдущей задаче. Сделаем это в два хода

\[\begin{equation*} \begin{aligned} & d = \frac{\partial L}{\partial \hat y} \\ & \frac{\partial L}{\partial W_3} = \frac{\partial L}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial W_3} = O_2^T \cdot d. \end{aligned} \end{equation*}\]

Матрица \(O_2^T\) будет размера \([2 \times n],\) вектор \(d\) будет размера \([n \times 1]\), размер производной будет \([2 \times 1],\) что совпадает с размером матрицы \(W_3.\)

Для поиска производной \(\frac{\partial L}{\partial W_2}\) переиспользуем значение, которое накопилось в \(d\)

\[\begin{equation*} \begin{aligned} & d = \frac{\partial L}{\partial H_2} = d \cdot \frac{\partial \hat y}{\partial O_2} \cdot \frac{\partial O_2}{\partial H_2} = d \cdot W_3^T * f'(H_2) \\ & \frac{\partial L}{\partial W_2} = O_1^T \cdot d. \end{aligned} \end{equation*}\]

Размер \(d\) был \([n \times 1],\) после персчёта стал \([n \times 1] \cdot [1 \times 2] * [n \times 2] = [n \times 2].\) Поэлементное умножение на производную функции активации не повлияло на размер матрицы. Размер производной \(\frac{\partial L}{\partial W_2}\) оказывается \([2 \times 2],\) что совпадает с размером матрицы \(W_2.\)

Осталась заключительная производная \(\frac{\partial L}{\partial W_1}\). Нам надо найти

\[\begin{equation*} \begin{aligned} & d = \frac{\partial L}{\partial H_1} = \frac{\partial L}{\partial H_2} \cdot \frac{\partial H_2}{\partial O_1} \cdot \frac{\partial O_1}{\partial H_1} = d \cdot W_2^T * f'(H_1)\\ & \frac{\partial L}{\partial W_1} = X^T \cdot d. \end{aligned} \end{equation*}\]

Если бы сетка была глубже, мы продолжили бы переиспользовать \(d\). Каждую производную мы посчитали один раз. Такой алгоритм обучения линеен по числу параметров.