1. Дропаут

Посещая свой банк я заметил, что операционисты, обслуживающие меня, часто меняются. Я спросил одного из них, почему так происходит. Он сказал, что не знает, но им часто приходится переходить с места на место. Я предположил, что это делается для исключения мошеннического сговора с сотрудником банка.

Это навело меня на мысль, что удаление случайно выбранного подмножества нейронов из каждого примера может помочь предотвратить заговор модели с исходными данными и ослабить эффект переобучения.

—Джеффри Хинтон

а) Опишите, как сделать через линейный слой с Dropout прямой шаг и обратный шаг.

Решение

Пусть на вход в нейрон идет одно наблюдение \(h_1\) размера \([1 \times d]\). Тогда линейный слой с функцией активации отрабатывает по формуле

\[ h_2 = f(h_1 \cdot W + b). \]

На выходе мы получаем вектор \(h_2\) размера \([1 \times k].\) У матрицы \(W\) размерность \([d \times k],\) у вектора констант \(b\) размер \([1 \times k].\) Получается, что в слое \(k\) нейронов.

Каждый из нейронов мы выключаем с вероятностью \(p\), то есть нам надо умножить получившийся вектор \(h_2\) поэлементно на вектор из \(k\) случайных величин \(d\). Каждая компонента вектора будет иметь распределение Бернулли

\[\begin{split} d_j = \begin{cases}0, &p \\ 1, & 1 - p. \end{cases} \end{split}\]

Обозначим символом \(\odot\) поэлементное умножение матриц. В итоге слой будет работать как

\[ h_2 = d \odot f(h_1 \cdot W + b). \]

Если на вход к нам пришла матрица \(H_1\) размера \([n \times d],\) тогда линейный слой с дропаутом будет отрабатывать как

\[ H_2 = D \odot f(H_1 \cdot W + b). \]

Матрица \(D\) состоит из нулей и единиц из распределения Бернулли.

Без дропаута шаг обратного распространения ошибки выглядит как

\[ \underset{[n \times k]}{\frac{\partial L}{\partial H_1}} = \underset{[n \times d]}{\frac{\partial L}{\partial H_2}} \cdot \underset{[d \times k]}{W^T} \odot \underset{[n \times k]}{f'(H_1 \cdot W + b)}. \]

В скобках подписаны размерности. Для слоя с дропаутом шаг обратного распространения ошибки выглядит как

\[ \underset{[n \times k]}{\frac{\partial L}{\partial H_1}} = \underset{[n \times d]}{\frac{\partial L}{\partial H_2}} \cdot \underset{[d \times k]}{W^T} \odot \underset{[n \times k]}{f'(H_1 \cdot W + b)} \odot \underset{[n \times k]}{D}. \]

Получается, что градиенты по занулившимся нейронам зануляются и сетка игнорирует их при шаге обратного распространения ошибки. Производная по весам слоя выглядит как

\[ \underset{[d \times k]}{\frac{\partial L}{\partial W}} = \underset{[d \times n]}{H_1^T} \cdot \underset{[n \times k]}{\frac{\partial L}{\partial H_1}} \]

Именно на эту величину делается шаг градиентного спуска.

б) Обычно Dropout добавляют в нейросеть, чтобы избежать переобучения. Объясните, как именно этот слой помогает в этом.

Решение

Дропаут позволяет бороться с коадаптацией нейронов. При обучении мы зануляем часть выходов, тем самым мы изменяем только часть параметров и нейроны учатся более независимо.

Более того, Хинтону и его соавторам удалось показать, что дропаут эквивалентен усреднению всех тех моделей, которые получались на каждом шаге случайным выбрасыванием отдельных нейронов. Иначе говоря, мы усредняем \(2^N\) возможных моделей, где \(N\) – число нейронов, которые могут быть выкинуты или оставлены.

в) Дропаут выплёвывает случайные выходы. Не очень понятно как применять слой на стадии тестирования. Пусть у нас есть два нейрона, каждый из которых мы отключаем с вероятностью \(0.4\).

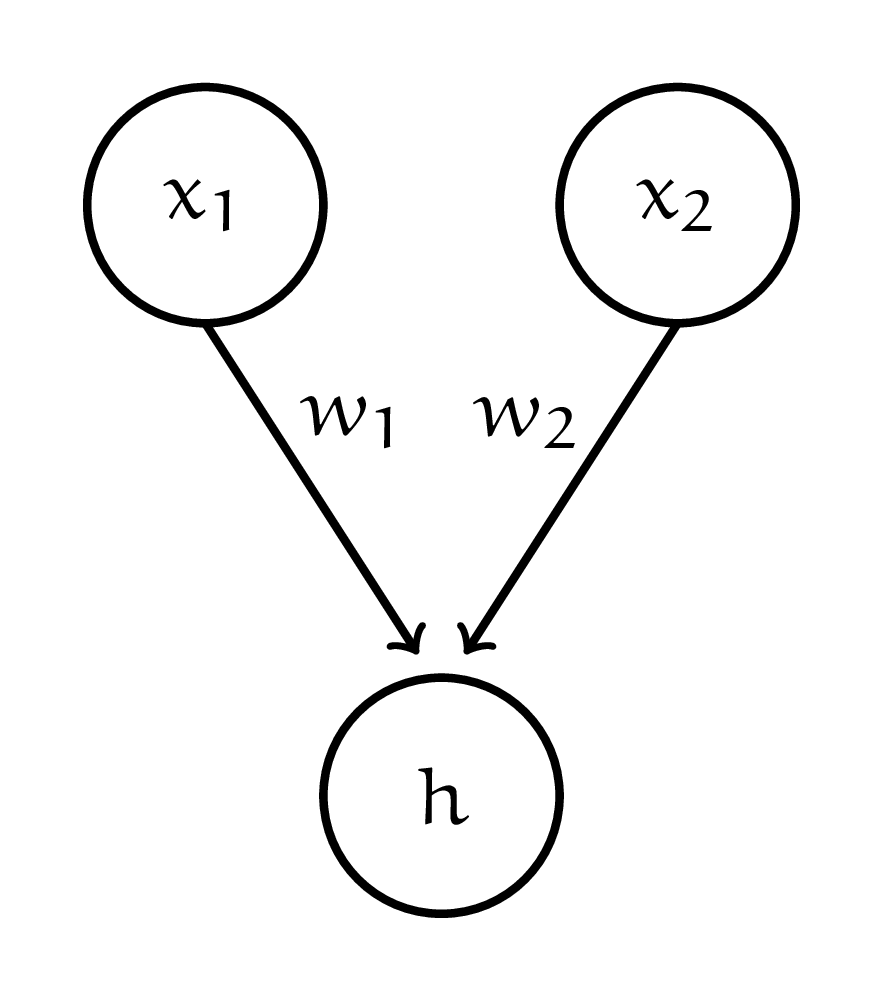
Нейроны выплёвывают \(x_1\) и \(x_2\). Дальше мы складываем их с весами \(w_1\) и \(w_2\) и поулучаем выход \(h\).

Один из способов использовать такую нейросеть на тесте – прогнать её при всех возможных вариантах реализации дропаута и усреднить получившиеся выходы. Проделайте это и найдите \(\mathbb{E}(h)\). Предложите более простой способ использовать нейросеть на тестовой выборке.

Решение

\[\begin{multline*} \mathbb{E}(h) = 0.6 \cdot 0.6 \cdot (w_1 \cdot x_1 + w_2 x_2) + 0.6 \cdot 0.4 \cdot (w_1 \cdot x_1 + 0 ) + \\ + 0.4 \cdot 0.6 \cdot (0 + w_2 x_2) + 0.4 \cdot 0.4 \cdot (0 + 0) = 0.6 \cdot (w_1 \cdot x_1 + w_2 x_2). \end{multline*}\]

Мы применяем дропаут с параметром \(0.4\). Достаточно просто домножить выход нейрона на \(0.6,\) и мы получим точно такой же результат, как при усреднении всех возможных выходов.

Получается, что нам надо поддерживать одну функцию для прогнозов на обучающей выборке без домножения на \(1 - p\) и одну функцию для прогнозов с домножением на \(1 - p\). Хочется избежать такого раздвоения.

г) Обычно, в нейросетях используют обратный дропаут. Прямой проход делается по формуле

\[ H_2 = \frac{1}{1- p} \cdot D \odot f(H_1 \cdot W + b). \]

Для обратного прохода производная также домножается на \(\frac{1}{1- p}\). Как думаете, почему используют именно такой вариант?

Решение

Чтобы посчитать прогноз на тесте для обычного дропаута, нам нужно умножить выход слой на \(1 - p\)

\[ H_2 = (1 - p) \cdot f(H_1 \cdot W + b). \]

Если мы будем умножать выход при обучении на \(\frac{1}{1- p},\) нам не надо будет при тестировании умножать выходы на \((1 - p).\)

д) Запишите шаг градиентного спуска для весов линейного слоя с обратным дропаутом и без него. Какой эффект оказывает обратный дропаут на скорость обучения?

Решение

Производная для линейного слоя без дропаута выглядит как

\[ \underset{[d \times k]}{\frac{\partial L}{\partial W}} = \underset{[d \times n]}{H_1^T} \cdot \underset{[n \times k]}{\frac{\partial L}{\partial H_1}}. \]

Шаг градиентного спуска выглядит как

\[ W_t = W_{t - 1} - \eta_t \cdot \frac{\partial L}{\partial W}(W_{t-1}). \]

Если мы добавляем дропаут, формула меняется на

\[ W_t = W_{t - 1} - \eta_t \cdot \frac{1}{1-p} \cdot \frac{\partial L}{\partial W}(W_{t-1}). \]

Получается, что скорость обучения дополнительно домножается на коэффициент \(\frac{1}{1-p} \ge 1.\) Получается, что величина шага увеличивается.

е) Предположим, что Маша решила после первого слоя добавить в свою сетку Dropout c вероятностью \(p\). Какова вероятность того, что отключится весь слой?

Пусть случайная величина \(N\) — это число включённых нейронов. Найдите её математическое ожидание и дисперсию. Если Маша хочет оставить четверть работающих нейронов, какое значение \(p\) она должна поставить?

Решение

Пусть у нас на слое \(k\) нейронов. Каждый отключается с вероятностью \(p,\) значит весь слой отключится с вероятностью \(p^k\).

Пусть \(Y_i = 1,\) если \(i-\)ый нейрон работает. Тогда \(\mathbb{E}(Y_i) = 1 - p\). Получается, что

\[ \mathbb{E}(N) = \mathbb{E}(Y_1 + \ldots + Y_k) = (1 - p) \cdot k. \]

Получается, что у \(N\) будет биномиальное распределение. Если мы хотим оставить только четверть работающих нейронов, нам нужна \(p = 0.75\).

ё) Маша добавила Dropout c вероятностью \(p\). после каждого из трёх слоёв нейросетки. Какова вероятность того, что один из слоёв отключится и сетка не сможет учиться?

Решение

Пусть у нас на первом слое \(k_1\) нейронов, на втором \(k_2\) нейронов, на третьем \(k_3\) нейронов. Слои умирают с вероятностями \(p^{k_1}, p^{k_2}, p^{k_3}.\)

Вероятность того, что не отключиться ни один слой составит

\[ q = (1 - p^{k_1}) \cdot (1 - p^{k_2}) \cdot (1 - p^{k_3}). \]

Получается, что хотябы один слой умрёт с вероятностью \(1 - q\).

ж) Функция активации SELU обладает свойством самонормализации. Если правильно инициализировать веса нейросети, выход линейного слоя с SELU всегда имеет нулевое среднее и единичное стандартное отклонение.

Градиентному спуску легче заниматься оптимизацией, когда данные нормализованы. Если мы в нейросеть добавим дропаут, нормализация испортится. Каким станет математическое ожидание и дисперсия в результате добавления дропаута? Подумайте, как это можно исправить.

Решение

В случае обратного дропаута, во время обучения, мы домножаем выход из слоя на \(d \sim \text{Bern}(1 - p)\) и на \(\frac{1}{1 - p}\)

\[ h = \frac{1}{1 - p} \cdot d \cdot x. \]

Выход нейросети \(x\) и дропаут \(d\) независимые случайные величины, получается среднее никак не меняется

\[ \mathbb{E}(h) = \mathbb{E} \left( \frac{1}{1 - p} \cdot d \cdot x \right) = \frac{1}{1 - p} \cdot \mathbb{E}(d) \cdot \mathbb{E}(x) = \mathbb{E}(x). \]

Дисперсия изменится

\[ \text{Var}(h) = \text{Var} \left( \frac{1}{1 - p} \cdot d \cdot x \right) = \frac{1}{(1 - p)^2} \cdot \text{Var}(d) \cdot \text{Var}(x) = \frac{p}{(1 - p)} \cdot \mathbb{E}(x). \]

Если мы будем домножать выход на \(\frac{1-p}{p}\), мы сломаем среднее. Более того, это изменит вероятность дропаута.

При нормализации мы сдвигаем случайную величину на какую-то константу и умножаем её на какую-то константу. По аналогии можно поступить с выходом из дропаута.

Примерно это делают авторы функции активации SELU в своей статье.[1] Не обходится без хитростей, взятых из воздуха.

Нам нужно нулевое математическое ожидание. Дропаут выдаёт на выход либо единицы либо нули, нулевого математического ожидания никак тут не получишь. Авторы говорят, что SELU в отрицательной области

\[ \lim_{t \to -\infty} SELU(t) = - \alpha \cdot \lambda = \alpha'. \]

Можно попробовать взять \(- \alpha'\) в качестве нового дефолтного значения для дропаута и заставить его работать по формуле

\[\begin{split} d(t) = \begin{cases}h, & 1 - p \\ \alpha', & p. \end{cases} \end{split}\]

Дальше нам надо сдвинуть выход слоя на константу \(b\) и умножить на константу \(a\)

\[ d(t) \cdot a + b \]

так, чтобы математическое ожидание и дисперсия не поменялись

\[\begin{align*} & \mathbb{E}(a \cdot (d \cdot x + (1 - d) \cdot \alpha') + b) = 0 \\ & \text{Var}(a \cdot (d \cdot x + (1 - d) \cdot \alpha') + b) = 1. \end{align*}\]

Решив эту систему уравнений, можно поулчить что

\[\begin{align*} & a = (p + (\alpha')^2 \cdot p \cdot (1 - p))^{-0.5} \\ & b = - (p + (\alpha')^2 \cdot p \cdot (1 - p))^{-0.5} \cdot ((1-p)\alpha'). \end{align*}\]

Такое преобразование оставит эффект разреженности от дропаута и сохранит нормализованные данные. Авторы называют его Alpha Dropout.

---

[1]

Mish: A Self Regularized Non-Monotonic Activation Function