1. Из авторегрессии в RNN

В самом начале этой книги мы выяснили, что нейросеть – это ансамбль регрессий. Линейная регрессия записывалась в виде одного уравнения

\[ y_i = b + w x_i. \]

Чтобы перейти от линейной регрессии к нейрону, мы завели скрытое состояние и применили к нему функцию активации

\[\begin{equation*} \begin{aligned} & h_i = b + w x_i \\ & y_i = f(h_i). \end{aligned} \end{equation*}\]

Авторегрессия – это простейшая линейная модель, которая позволяет работать с последовательностями. Мы в ней пытаемся объяснить текущее значение ряда через предыдущее

\[ y_t = b + w y_{t-1}. \]

Можно изобразить такую модель на картинке следующим образом:

Давайте попробуем перейти от неё к рекуррентному нейрону по аналогии с линейной моделью. На картинке рекурретный нейрон можно изобразить следующим образом:

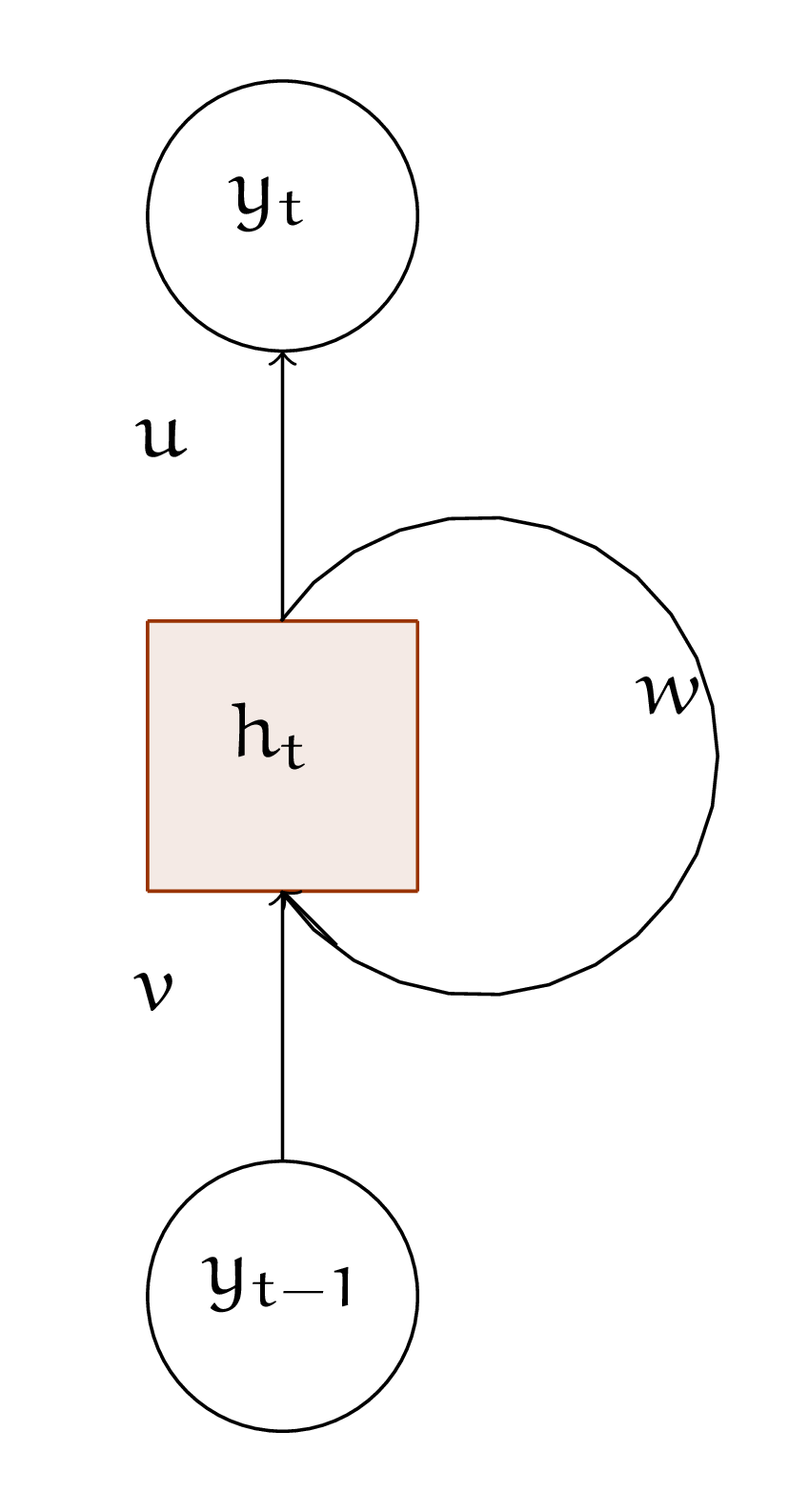
Выпишите уравнения, описывающие рекуррентный нейрон. На картинке не отмечены места, где используются функции активации. Додумайте сами, где в уравнениях нужна нелинейность. Можно ли ограничиться только одним уравнением?

Решение

Если мы выпишем уравнения чисто по картинке, то получим

\[\begin{equation*} \begin{aligned} & h_t = b_h + v \cdot y_{t-1} + w \cdot h_{t-1} \\ & y_t = b_y + u \cdot h_t. \end{aligned} \end{equation*}\]

В первом уравнении обновляется скрытое состояние нейрона. Оно учитывает в себе информацию обо всём, что до этого происходило в последовательности. Во втором уравнении на базе скрытого состояния мы строим прогноз.

Из-за того, что скрытое состоянии теперь зависит от времени, одним уравнением ограничиться не получится. Нам надо на каждом шаге обновлять его, а затем строить прогноз.

Пока что перед нами линейная модель. Давайте добавим в неё нелинейность. Для этого к каждому из уравнений применим функцию активации и получим уравнения, описывающие RNN-ячейку

\[\begin{equation*} \begin{aligned} & h_t = f_h(b_h + v \cdot y_{t-1} + w \cdot h_{t-1}) \\ & y_t = f_y(b_y + u \cdot h_t). \end{aligned} \end{equation*}\]

В принципе, для прогнозирования необязательно применять функцию активации, но если мы это сделаем, модель станет более выразительной.