2. Придумываем бэкпроп

У Маши есть нейросеть с картинки ниже, где \(w_k\) — вес для \(k\)-го слоя, \(f(t)\) — какая-то функция активации. Маша хочет научиться делать для такой нейронной сетки градиентный спуск.

а) Запишите Машину нейросеть, как сложную функцию.

Решение

Чтобы записать нейросеть как сложную функцию, нужно просто последовательно применить все слои

\[ \hat y_i = f(f(x_i \cdot w_1) \cdot w_2) \cdot w_3. \]

б) Предположим, что Маша решает задачу регрессии. Она прогоняет через нейросетку одно наблюдение. Она вычисляет знчение функции потерь \(L(w_1, w_2, w_3) = \frac{1}{2} \cdot (y - \hat y)^2\). Найдите производные функции \(L\) по всем весам \(w_k\).

Решение

Запишем функцию потерь и аккуратно найдём все производные

\[ L(w_1, w_2, w_3) = \frac{1}{2} \cdot (y - \hat y)^2 = \frac{1}{2} \cdot (y - f(f(x \cdot w_1) \cdot w_2) \cdot w_3)^2. \]

Делаем это по правилу взятия производной сложной функции

\[\begin{equation*} \begin{aligned} & \frac{\partial L}{\partial w_3} = \frac{\partial L}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial w_3} = (y - \hat{y}) \cdot f(f(x\cdot w_1) \cdot w_2) \\ & \frac{\partial L}{\partial w_2} = \frac{\partial L}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial w_2} = (y - \hat{y}) \cdot w_3 \cdot f'(f(x\cdot w_1) \cdot w_2) \cdot f(x\cdot w_1) \\ & \frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial w_1} = (y - \hat{y}) \cdot w_3 \cdot f'(f(x\cdot w_1) \cdot w_2) \cdot w_2 \cdot f'(x\cdot w_1) \cdot x \\ \end{aligned} \end{equation*}\]

в) В производных повторяются одни и те же части. Постоянно искать их не очень оптимально. Выделите эти части в прямоугольнички.

Решение

Выделим в прямоугольники части, которые каждый раз считаются заново, хотя могли бы переиспользоваться.

\[\begin{equation*} \begin{aligned} & \frac{\partial L}{\partial w_3} = \frac{\partial L}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial w_3} = \boxed{ (y - \hat{y}) } \cdot f(f(x\cdot w_1) \cdot w_2) \\ & \frac{\partial L}{\partial w_2} = \frac{\partial L}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial w_2} = \boxed{ (y - \hat{y})} \cdot \boxed{ w_3 \cdot f'(f(x\cdot w_1) \cdot w_2)} \cdot f(x\cdot w_1) \\ & \frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial w_1} = \boxed{ (y - \hat{y}) } \cdot \boxed{ w_3 \cdot f'(f(x\cdot w_1) \cdot w_2)} \cdot w_2 \cdot f'(x\cdot w_1) \cdot x \\ \end{aligned} \end{equation*}\]

Если бы слоёв было бы больше, переиспользования возникали бы намного чаще. Градиентный спуск при таком подходе мы могли бы сделать точно также, как и в любых других моделях

\[\begin{equation*} \begin{aligned} & w_3^t = w_3^{t-1} - \eta \cdot \frac{\partial L}{\partial w_3}(w_3^{t-1}) \\ & w_2^t = w_2^{t-1} - \eta \cdot\frac{\partial L}{\partial w_2}(w_2^{t-1}) \\ & w_1^t = w_1^{t-1} - \eta \cdot\frac{\partial L}{\partial w_1}(w_1^{t-1}). \end{aligned} \end{equation*}\]

Проблема в том, что такой подход из-за постоянных перевычислений будет работать долго, за \(O(m^2)\), где \(m\) – глубина нейронной сетки. Алгоритм обратного распространения ошибки помогает более аккуратно считать производную и ускорить обучение нейросетей.

г) Выпишите все производные в том виде, в котором их было бы удобно использовать для алгоритма обратного распространения ошибки, а затем, сформулируйте сам алгоритм. Нарисуйте под него удобную схемку.

Решение

Выпишем алгоритм обратного распространения ошибки. Договоримся до следующих обозначений. Буквами \(h^k\) будем обозначать выход \(k-\)го слоя до применения функции активации. Буквами \(o^k\) будем обозначать выход после применения функции активации. Например, для первого слоя:

\[\begin{equation*} \begin{aligned} & h^1_i = w_1 \cdot x_i \\ & o^1_i = f(h_i^1). \\ \end{aligned} \end{equation*}\]

Сначала мы делаем прямой проход по нейросети (forward pass):

Наша нейросеть — граф вычислений. Давайте запишем для каждого ребра в рамках этого графа производную.

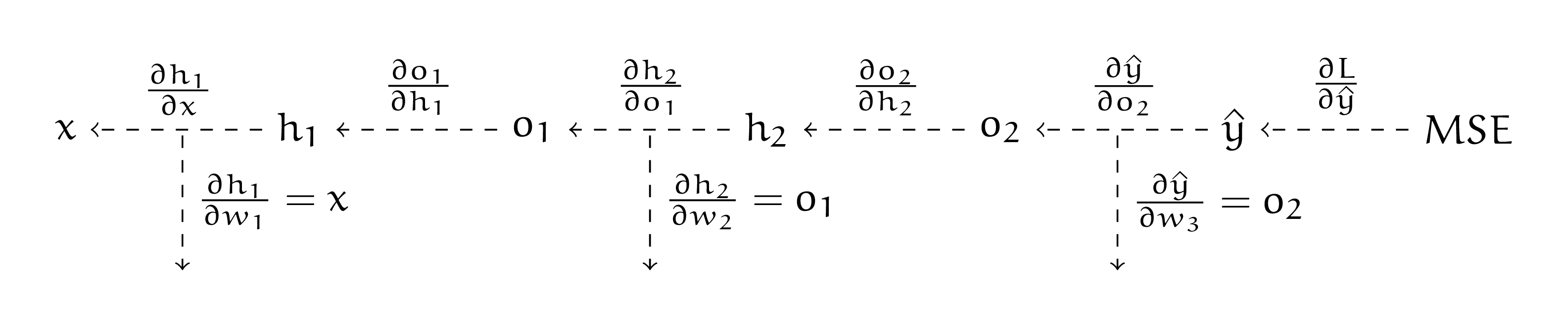
Мы везде работаем со скалярами. Все производные довольно просто найти по графу, на котором мы делаем прямой проход. Например,

\[ \frac{\partial h_2}{\partial w_2} = \frac{\partial (o_1 \cdot w_2)}{\partial w_2} = o_1. \]

Если в качестве функции активации мы используем сигмоиду

\[ f(z) = \sigma(z) = \frac{1}{1 + e^{-z}} = \frac{e^z}{1 + e^{z}}, \]

тогда

\[\begin{multline*} \frac{\partial \sigma }{\partial z} = \left(\frac{e^z}{1 + e^{z}} \right)' = \frac{e^z}{1 + e^{z}} - \frac{e^z}{(1 + e^{z})^2} \cdot e^z = \\ = \frac{e^z}{1 + e^{z}} \left(1 - \frac{e^z}{1 + e^{z}} \right) = \sigma(z)(1 - \sigma(z)). \end{multline*}\]

Получается, что

\[ \frac{\partial o_2}{\partial h_2} = \sigma'(h_2) = \sigma(h_2) \cdot (1 - \sigma(h_2)) = o_2 \cdot (1 - o_2). \]

Осталось только аккуратно записать алгоритм. В ходе прямого прохода мы запоминаем все промежуточные результаты. Они нам пригодятся для поиска производных при обратном проходе. Например, выше, в сигмоиде, при поиске производной, используется результат прямого прохода \(o_2.\)

Заведём для накопленного значения производной переменную \(d\). На первом шаге нам надо найти \(\frac{\partial L}{\partial w_3}\). Сделаем это в два хода

\[\begin{equation*} \begin{aligned} & d = \frac{\partial L}{\partial \hat y} \\ & \frac{\partial L}{\partial w_3} = d \cdot o_2. \end{aligned} \end{equation*}\]

Для поиска производной \(\frac{\partial L}{\partial w_2}\) переиспользуем значение, которое накопилось в \(d\). Нам надо найти

\[ \frac{\partial L}{\partial w_2} = \frac{\partial L}{\hat y} \cdot \frac{\partial \hat y}{\partial o_2} \cdot \frac{\partial o_2}{\partial h_2} \cdot \frac{\partial h_2}{\partial w_2} = d \cdot \boxed{ \frac{\partial \hat y}{\partial o_2} \cdot \frac{\partial o_2}{\partial h_2} } \cdot \frac{\partial h_2}{\partial w_2}. \]

Часть, выделенную в прямоугольник мы будем переиспользовать для поиска \(\frac{\partial L}{\partial w_1}\). Хорошо бы дописать её в \(d\) для этого. Получается, вторую производную тоже надо найти в два хода

\[\begin{equation*} \begin{aligned} & d = d \cdot \frac{\partial \hat y}{\partial o_2} \cdot \frac{\partial o_2}{\partial h_2} \\ & \frac{\partial L}{\partial w_2} = d \cdot o_1. \end{aligned} \end{equation*}\]

Осталась заключительная производная \(\frac{\partial L}{\partial w_1}\). Нам надо найти

\[ \frac{\partial L}{\partial w_2} = \frac{\partial L}{\hat y} \cdot \frac{\partial \hat y}{\partial o_2} \cdot \frac{\partial o_2}{\partial h_2} \cdot \frac{\partial h_2}{\partial o_1} \cdot \frac{\partial o_1}{\partial h_1} \cdot \frac{\partial h_1}{\partial w_1} = d \cdot \frac{\partial h_2}{\partial o_1} \cdot \frac{\partial o_1}{\partial h_1} \cdot \frac{\partial h_1}{\partial w_1}. \]

Снова делаем это в два шага

\[\begin{equation*} \begin{aligned} & d = d \cdot \frac{\partial h_2}{\partial o_1} \cdot \frac{\partial o_1}{\partial h_1} \\ & \frac{\partial L}{\partial w_1} = d \cdot x. \end{aligned} \end{equation*}\]

Если бы нейросетка была бы глубже, мы смогли бы переиспользовать \(d\) на следующих слоях. Каждую производную мы нашли ровно один раз. Это и есть алгоритм обратного распространения ошибки. Одна его итерация отрабатывает за \(O(m),\) где \(m\) – глубина нейронной сетки. В случае матриц происходит всё ровно то же самое, но дополнительно надо проследить за всеми размерностями и более аккуратно перемножить матрицы.