2. Туда и обратно

Маша хочет сделать шаг обратного распространения ошибки через рекуррентную ячейку для последовательности \(y_0 = 0, y_1=1, y_2 = -1, y_3 =2\). Скрытое состояние инициализировано как \(h_0 = 0\). Все веса инициализированы как \(0.5\). Во всех уравнениях, описывающих ячейку нет констант. В качестве функций активаций Маша использует \(ReLU\). В качестве функции потерь Маша использует \(MSE\).

а) Сделайте прямой шаг через ячейку. Для каждого элемента последовательности постройте прогноз. Посчитайте значение ошибки.

Решение

Рекуррентную сеть можно рассматривать, как несколько копий одной и той же сети, каждая из которых передает информацию последующей копии. Веса для всех копий одинаковые.

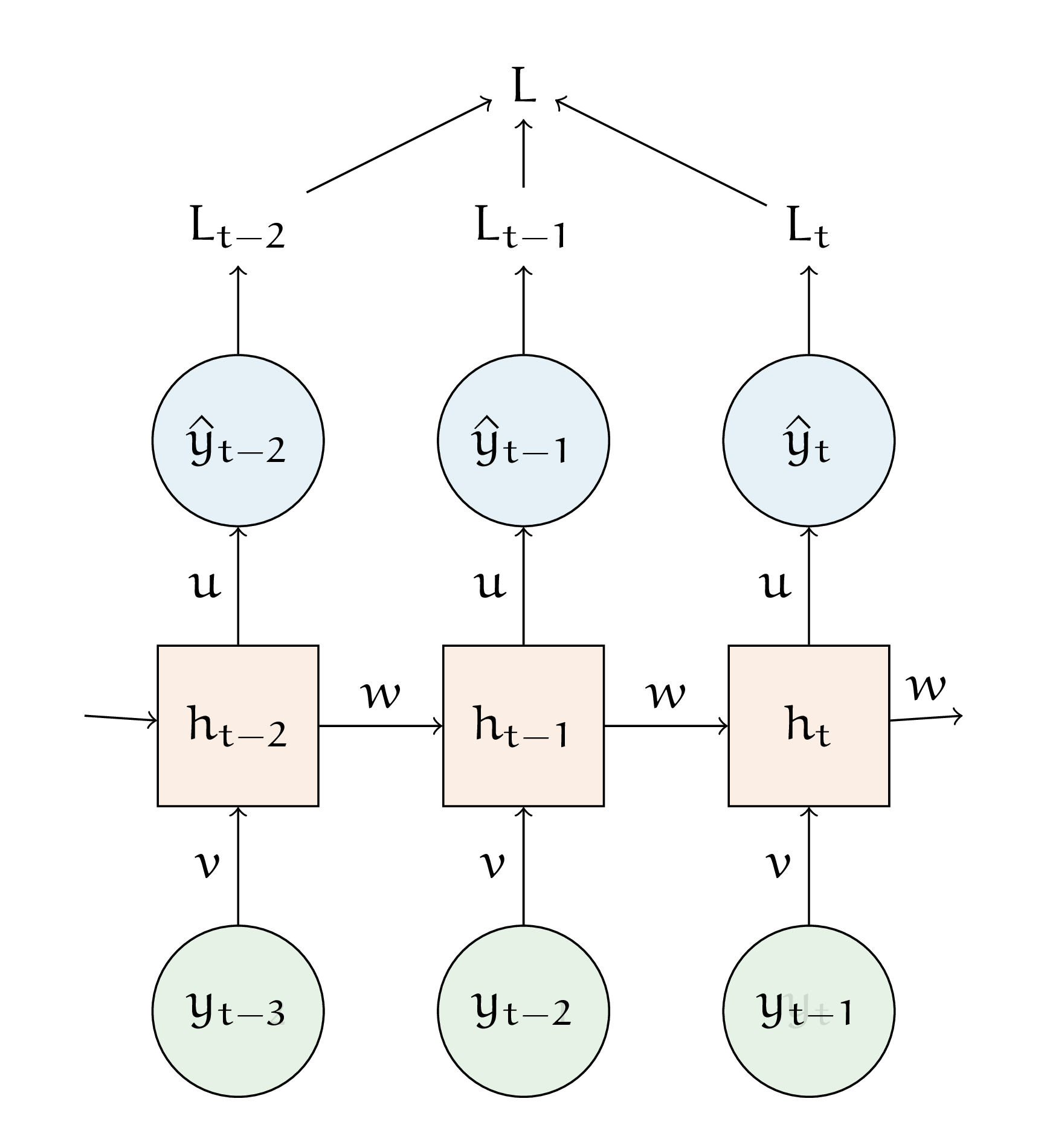
Когда мы строим прогнозы, мы движемся слева направо и сверху вниз. Чтобы сделать прямой шаг, нам нужно подставить соотвествуюшие значения в формулы пересчёта

\[\begin{equation*} \begin{aligned} h_t =& Relu(0.5 \cdot h_{t-1} + 0.5 \cdot y_{t-1})\\ \hat{y_t} =& Relu(0.5 \cdot h_t). \end{aligned} \end{equation*}\]

Тогда мы получим

\(t\)	\(0\)	\(1\)	\(2\)	\(3\)
\(h_t\)	\(0\)	\(0\)	\(0.5\)	\(0.375\)
\(\hat y_t\)	-	\(0\)	\(0.25\)	\(0.1875\)
\(y_t\)	\(0\)	\(1\)	\(-1\)	\(2\)
\(L_t\)	-	\(1\)	\(1.5625\)	\(3.285\)

Получаем итоговое значение ошибки нашего нейрона на всей последовательности

\[ L = L_1 + L_2 + L_3 = 1 + 1.5625 + 3.285 = 5.8475. \]

Именно его нам надо будет уменьшать в ходе обратного распространения ошибки.

б) Выпишите для рекуррентного нейрона производные функции ошибки по весам \(u,v,w\).

Решение

Выведем формулы для шага по весам \(u\). Нам нужно найти производную \(\frac{\partial L}{\partial u}\). Итоговая ошибка ищется как сумма ошибок на каждом элементе последовательности.

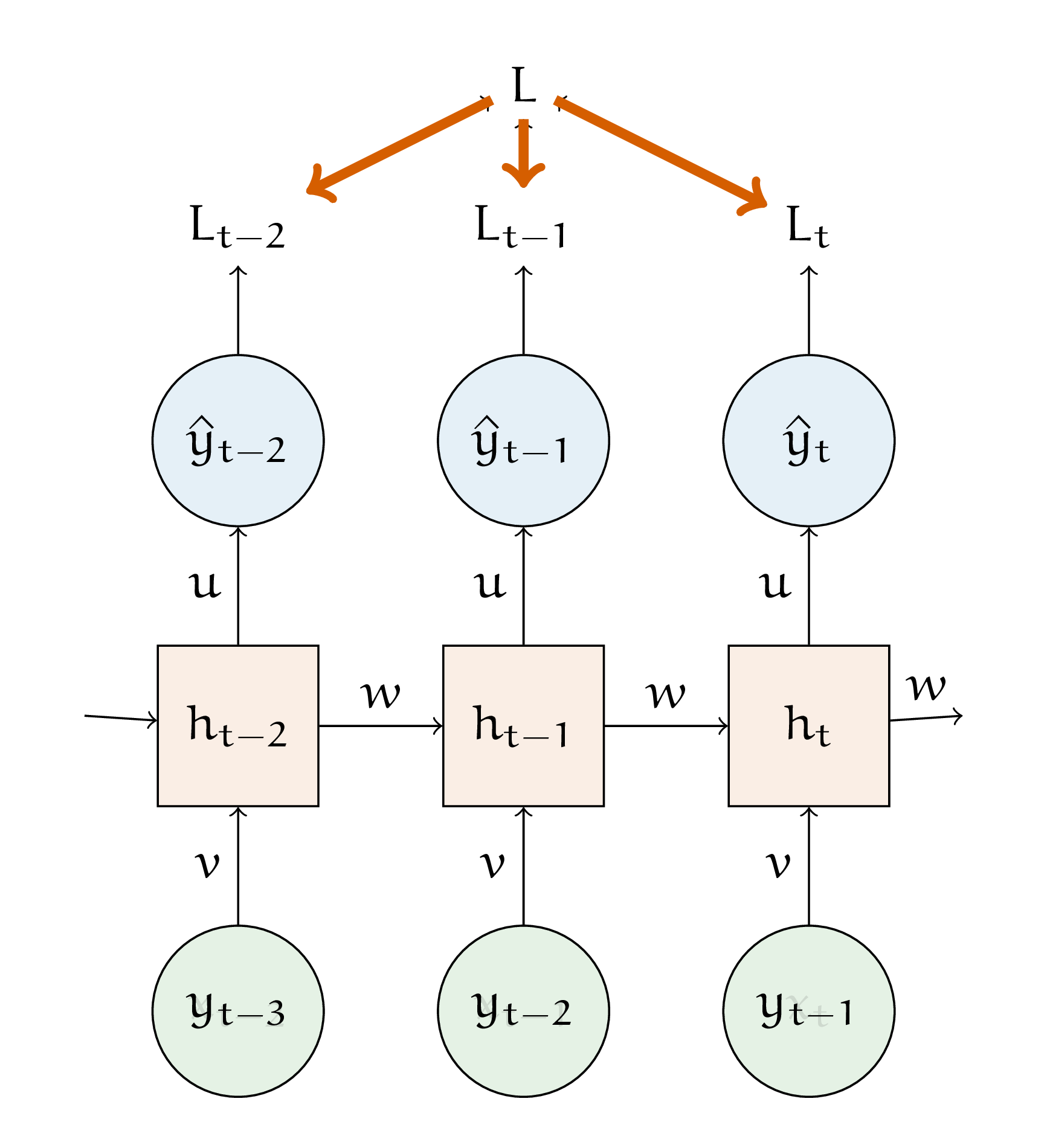
Это означает, что наша производная разваливается в сумму производных

\[ \frac{\partial L}{\partial u} = \sum_{t=0}^T \frac{\partial L_t}{\partial u}. \]

Посмотрим на одно слагаемое.

Для него производную можно расписать через предыдущие элементы нашего графа вычислений

\[ \frac{\partial L_t}{\partial u} = \frac{\partial L_t}{\partial \hat{y}_t} \cdot \frac{\partial \hat{y}_t}{\partial u}. \]

Все эти производные можно найти, если вспомнить формулы рекуррентного нейрона

\[\begin{equation*} \begin{aligned} h_t =& f_h(b_h +w \cdot h_{t-1} + v \cdot y_{t-1})\\ \hat{y}_t =& f_y(b_y + {\color{blue} u} \cdot h_t). \end{aligned} \end{equation*}\]

Параметр \(u\) присутствует в уравнении только в формуле для \(y\). Внутри \(h_t\) этот вес нигде не встречается, из-за этого производная оказывается простой

\[ \frac{\partial L_t}{\partial u} = \frac{\partial L_t}{\partial \hat{y}_t} \cdot f'_y(\ldots) \cdot h_t \]

Теперь найдём производную по весу \(w\).

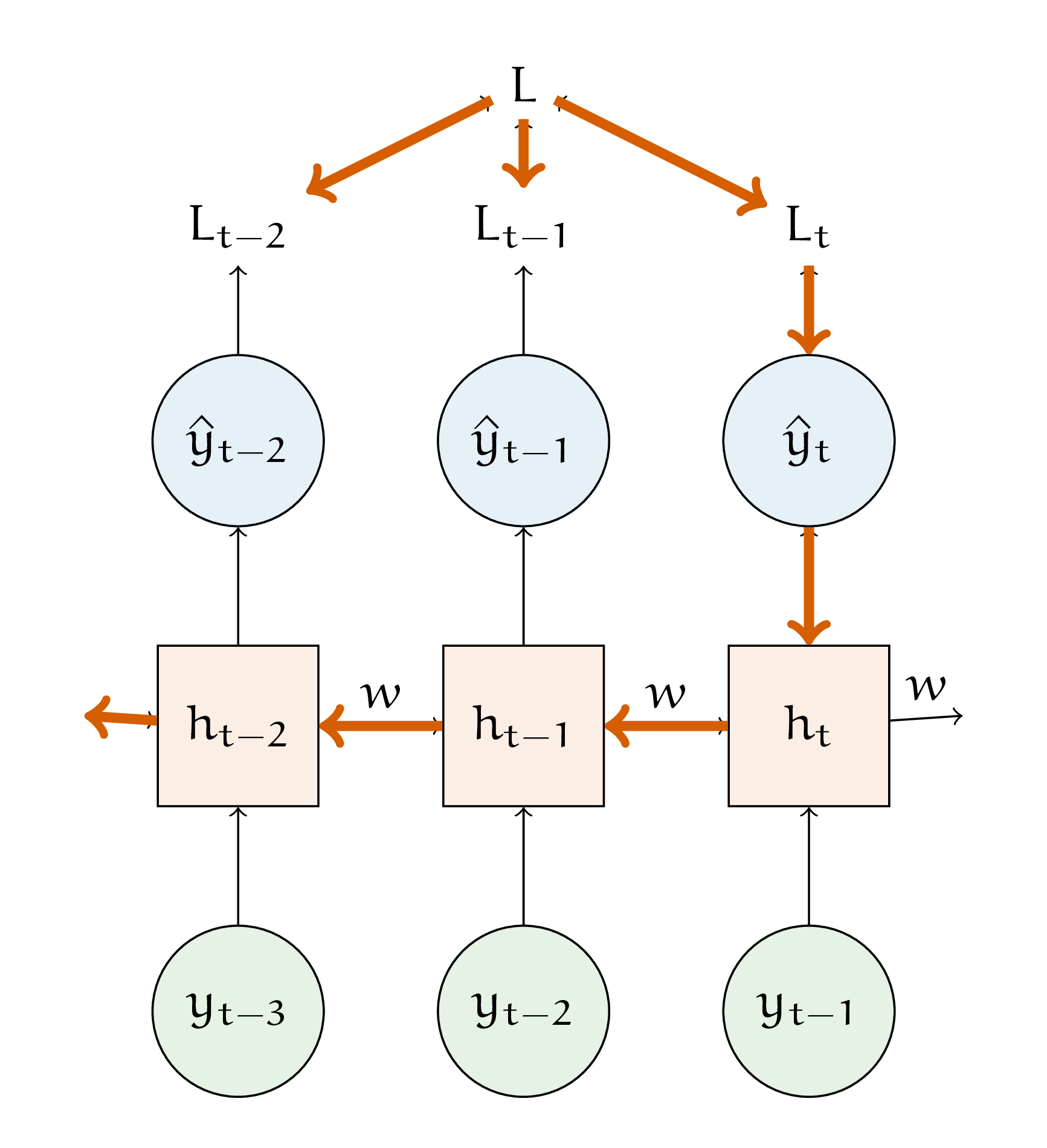
С этим весом возникнут проблемы, так как он участвует в каждом пересчёте \(h_t\). Придется брать производную назад во времени (backpropagation through time)

\[ \frac{\partial L_t}{\partial w} = \frac{\partial L_t}{\partial \hat{y}_t} \cdot \frac{\partial \hat{y}_t}{\partial h_t} \cdot {\color{blue} \frac{\partial h_t}{\partial w}}. \]

В формулах пересчёта вес \(w\) стоит перед \(h_{t-1},\) которая тоже зависит от \(w\)

\[\begin{equation*} \begin{aligned} h_t =& f_h(b_h + {\color{blue} w \cdot h_{t-1} }+ v \cdot y_{t-1})\\ \hat{y}_t =& f_y(b_y + u \cdot h_t). \end{aligned} \end{equation*}\]

Значит надо найти \(\frac{\partial h_{t-1}}{\partial w},\) которая будет зависеть от \(h_{t-2}\), которая тоже зависит от \(w\) и так далее

\[ \frac{\partial h_t}{\partial w} = \frac{\partial h_t}{\partial w} + \frac{\partial h_t}{\partial h_{t-1}} \cdot \frac{\partial h_{t-1}}{\partial w} + \ldots \]

Итоговая производная имеет вид

\[ \frac{\partial L_t}{\partial w} = \frac{\partial L_t}{\partial \hat{y}_t} \cdot \frac{\partial \hat{y}_t}{\partial h_t} \cdot \sum_{i=0}^t \left( \prod_{i=k+1}^t \frac{\partial h_i}{\partial h_{i-1}} \right) \cdot \frac{\partial h_k}{\partial w}. \]

Осталась заключительная производная по весу \(v\)

\[ \frac{\partial L_t}{\partial v} = \frac{\partial L_t}{\partial \hat{y}_t} \cdot \frac{\partial \hat{y}_t}{\partial h_t} \cdot \frac{\partial h_t}{\partial v}. \]

В ходе взятия этой производной мы нигде не упираемся в \(h_{t-1},\) поэтому назад во времени идти не нужно. Давайте подставим соотвествующие части уравнений и получим ответ

\[ \frac{\partial L_t}{\partial v} = \frac{\partial L_t}{\partial \hat{y}_t} \cdot f'_y(\ldots) \cdot u \cdot f'_h(\ldots) \cdot y_{t-1} \]

в) Сделайте шаг обратного распространения ошибки по весу \(u\)

Решение

Итак

\[ \frac{\partial L}{\partial u} = \frac{\partial L_1}{\partial u} + \frac{\partial L_2}{\partial u} + \frac{\partial L_3}{\partial u}, \]

где

\[\begin{equation*} \begin{aligned} & \frac{\partial L_1}{\partial u} = \frac{\partial L_1}{\partial \hat{y}} \cdot f'(\ldots) \cdot h_1 = -2 \cdot (1 - 0) \cdot 0 \cdot 0 = 0 \\ & \frac{\partial L_2}{\partial u} = \frac{\partial L_2}{\partial \hat{y}} \cdot f'(\ldots) \cdot h_2 = -2 \cdot (-1 - 0.25) \cdot 1 \cdot 0.5 = 1.25 \\ & \frac{\partial L_3}{\partial u} = \frac{\partial L_3}{\partial \hat{y}} \cdot f'(\ldots) \cdot h_3 = -2 \cdot (2 - 0.1875) \cdot 1 \cdot 0.375 = -1.36. \end{aligned} \end{equation*}\]

Получается, что

\[ \frac{\partial L}{\partial U} = \frac{\partial L_1}{\partial U} + \frac{\partial L_2}{\partial U} + \frac{\partial L_3}{\partial U} = 0 + 1.25 - 1.36 = -0.11 \]

В итоге

\[ u_1 = u_0 - \gamma \cdot \frac{\partial L}{\partial u} = 0.5 - 0.1 \cdot (-0.11) = 0.511 \]

По весам \(w\) и \(v\) также можно сделать шаг обратного распространения ошибки, но расчёты будут более неприятными.

г) Как изменится нейрон, если на вход в него будет идти не одна последовательность, а несколько?

Решение

В таком случае все веса превратятся в матрицы. Формулы останутся теми же самыми.