6. Бэкпроп своими руками

У Маши есть нейросеть с картинки ниже. Она использует функцию потерь

\[ L(W_1, W_2, W_3) = \frac{1}{2} \cdot (\hat y - y)^2. \]

В качестве функции активации Маша выбрала сигмоиду \(\sigma(t) = \frac{e^t}{1 + e^t}\).

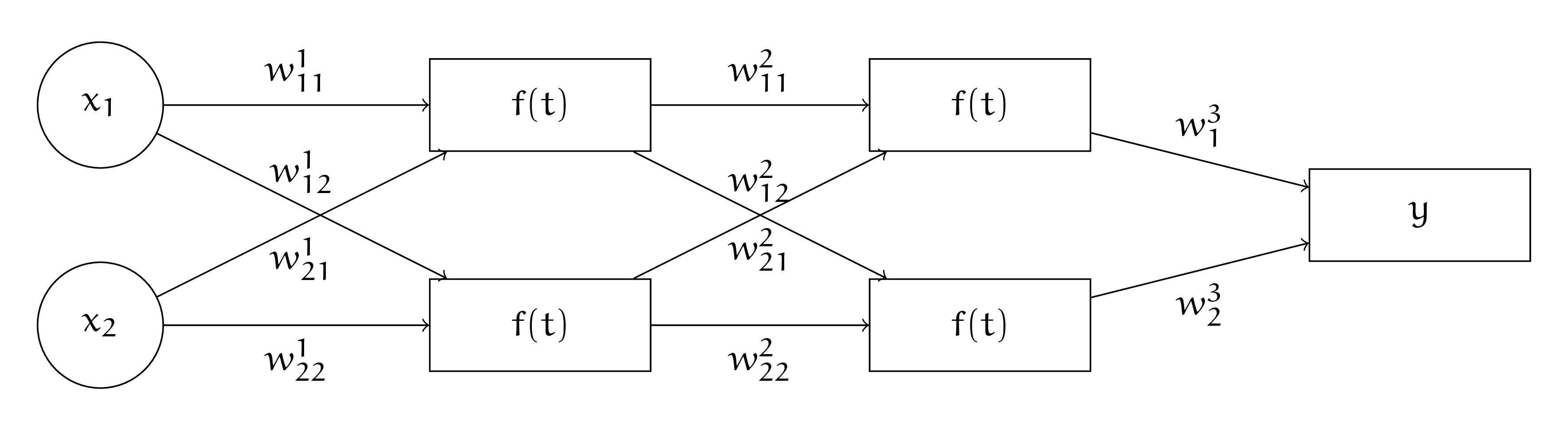
Выпишите для Машиной нейросетки алгоритм обратного распространения ошибки в общем виде. Пусть Маша инициализировала веса нейронной сети нулями. У неё есть два наблюдения.

Первое: \(x_1 = 1, x_2 = 1, y = 0\). И второе: \(x_1 = 5, x_2 = 2, y = 1\).

Сделайте руками два шага алгоритма обратного распространения ошибки. Пусть скорость обучения \(\eta = 1\). Стохастический градиентный спуск решил, что сначала для шага будет использоваться второе наблюдение, а затем первое.

Решение

Для начала запишем алгоритм в общем виде. Для этого нам надо взять схему из предыдущей задачи и записать там все производные. Для сигмоиды \(\sigma'(t) = \sigma(t) \cdot (1 - \sigma(t)).\) Прямой проход по нейронной сети (forward pass):

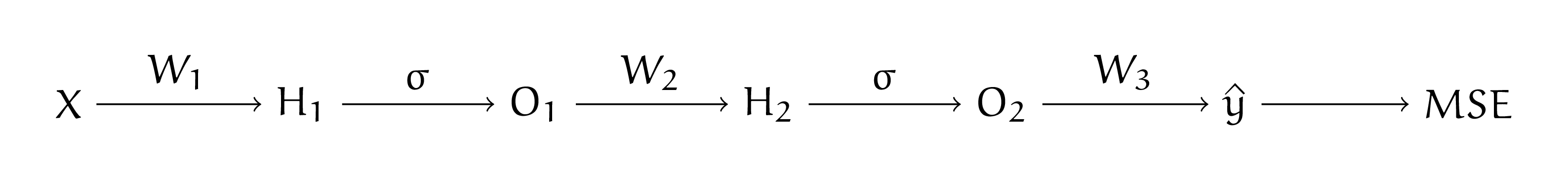
Обратный проход по нейронной сети (backward pass):

По аналогии с предыдущей задачей выпишем формулы для обратного распространения ошибки. На третьем слое:

\[\begin{equation*} \begin{aligned} & d = (\hat{y} - y) \\ & \frac{\partial MSE}{\partial W_3} = O_2^T \cdot d \\ \end{aligned} \end{equation*}\]

На втором слое:

\[\begin{equation*} \begin{aligned} & d = d \cdot W_3^T \odot O_2 \odot (1 - O_2) \\ & \frac{\partial MSE}{\partial W_2} = O_1^T \cdot d \\ \end{aligned} \end{equation*}\]

На первом слое:

\[\begin{equation*} \begin{aligned} & d = d \cdot W_2^T \odot O_1 \odot (1 - O_1) \\ & \frac{\partial MSE}{\partial W_1} = X^T \cdot d \\ \end{aligned} \end{equation*}\]

Когда мы аккуратно подставим все числа, можно будет сделать шаг SGD

\[\begin{equation*} \begin{aligned} & W_3^t = W_3^{t-1} - \eta \cdot \frac{\partial MSE}{\partial W_3} \\ & W_2^t = W_2^{t-1} - \eta \cdot \frac{\partial MSE}{\partial W_2} \\ & W_1^t = W_1^{t-1} - \eta \cdot \frac{\partial MSE}{\partial W_1} \\ \end{aligned} \end{equation*}\]

Сделаем шаг SGD для второго наблюдения. Делаем прямое распространение для второго наблюдения, напомним, что матрицы весов инициализированы нулями:

Делаем обратный проход.

Шаг 1:

\[\begin{equation*} \begin{aligned} & d = (\hat{y} - y) = -1 \\ & \frac{\partial MSE}{\partial W_3} = O_2^T \cdot d = \begin{pmatrix} 0.5 \\ 0.5 \end{pmatrix} \cdot (-1) = \begin{pmatrix} -0.5 \\ -0.5 \end{pmatrix} \\ \end{aligned} \end{equation*}\]

Шаг 2:

\[\begin{equation*} \begin{aligned} & d = d \cdot W_3^T * O_2 * (1 - O_2) = -1 \cdot (0, 0) \odot (0.5, 0.5) \odot (0.5, 0.5) = (0, 0) \\ & \frac{\partial MSE}{\partial W_2} = O_1^T \cdot d = \begin{pmatrix} 0.5 \\ 0.5 \end{pmatrix} \cdot (0, 0) = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \\ \end{aligned} \end{equation*}\]

Шаг 3:

\[\begin{equation*} \begin{aligned} & d = d \cdot W_2^T \odot O_1 \odot (1 - O_1) = (0, 0) \cdot \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \odot (0.5, 0.5) \odot (0.5, 0.5) = (0, 0) \\ & \frac{\partial MSE}{\partial W_1} = X^T \cdot d = \begin{pmatrix} 5 \\ 2 \end{pmatrix} \cdot (0, 0) = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \\ % & W_1^1 = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} - 1 \cdot \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \end{aligned} \end{equation*}\]

Делаем шаг градиентного спуска

\[\begin{equation*} \begin{aligned} & W_1^1 = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} - 1 \cdot \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}\\ & W_2^1 = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} - 1 \cdot \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \\ & W_3^1 = \begin{pmatrix} 0 \\ 0 \end{pmatrix} - 1 \cdot \begin{pmatrix} -0.5 \\ -0.5 \end{pmatrix} = \begin{pmatrix} 0.5 \\ 0.5 \end{pmatrix} \end{aligned} \end{equation*}\]

Сделаем шаг SGD для первого наблюдения. Делаем прямое распространение для второго наблюдения, напомним, что матрицы весов инициализированы нулями:

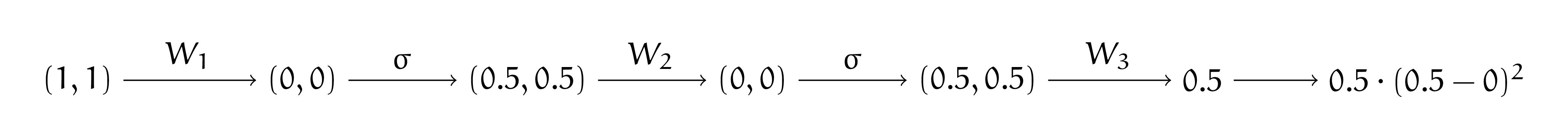
Делаем обратный проход.

Шаг 1:

\[\begin{equation*} \begin{aligned} & d = (\hat{y} - y) = 0.5 \\ & \frac{\partial MSE}{\partial W_3} = O_2^T \cdot d = \begin{pmatrix} 0.5 \\ 0.5 \end{pmatrix} \cdot (0.5) = \begin{pmatrix} 0.25 \\ 0.25 \end{pmatrix} \\ \end{aligned} \end{equation*}\]

Шаг 2:

\[\begin{equation*} \begin{aligned} & d = d \cdot W_3^T \odot O_2 \odot (1 - O_2) = 0.5 \cdot (0.5, 0.5) \odot (0.5, 0.5) \odot (0.5, 0.5) = (1/16, 1/16) \\ & \frac{\partial MSE}{\partial W_2} = O_1^T \cdot d = \begin{pmatrix} 0.5 \\ 0.5 \end{pmatrix} \cdot (1/16, 1/16) = \begin{pmatrix} 1/32 & 1/32 \\ 1/32 & 1/32 \end{pmatrix} \\ \end{aligned} \end{equation*}\]

Шаг 3:

\[\begin{equation*} \begin{aligned} & d = d \cdot W_2^T \odot O_1 \odot (1 - O_1) = (1/16, 1/16) \cdot \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \odot (0.5, 0.5) \odot (0.5, 0.5) = (0, 0) \\ & \frac{\partial MSE}{\partial W_1} = X^T \cdot d = \begin{pmatrix} 1 \\ 1 \end{pmatrix} \cdot (0, 0) = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \\ \end{aligned} \end{equation*}\]

На этой задаче видно, как сигмоида способствует затуханию градиента. Её производная по абсолютной величине всегда принимает значения меньше \(1\). Из-з этого значение \(d\) от слоя к слою становится всё меньше и меньше. Чем ближе к началу нашей сети мы находимся, тем на меньшую величину шагают веса. Если сетка оказывается очень глубокой, такой эффект ломает её обучение. Его обычно называют \indef{параличом нейронной сети.} Именно из-за этого сигмоиду обычно не используют в глубоких архитектурах.

Делаем шаг градиентного спуска

\[\begin{equation*} \begin{aligned} & W_3^2 = \begin{pmatrix} 0.5 \\ 0.5 \end{pmatrix} - 1 \cdot \begin{pmatrix} 0.25 \\ 0.25 \end{pmatrix} = \begin{pmatrix} 0.25 \\ 0.25 \end{pmatrix} \\ & W_2^2 = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} - 1 \cdot \begin{pmatrix}1/32 & 1/32 \\ 1/32 & 1/32 \end{pmatrix} = \begin{pmatrix} -1/32 & -1/32 \\ -1/32 & -1/32 \end{pmatrix} \\ & W_1^1 = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} - 1 \cdot \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \end{aligned} \end{equation*}\]

Объясните, почему инициализировать веса нулями — плохая идея. Почему делать инициализацию весов любой другой константой — плохая идея?

Решение

Из-за того, что мы инициализировали веса нулями, слои поначалу учатся по-очереди. Пока мы не сдвинем веса более поздних слоёв, веса более ранних слоёв не сдвинутся. Это замедляет обучение. Обратите внимание, что все веса меняются на одну и ту же величину в одном и том же направлении.

При инициализации любой другой константой этот эффект сохраниться. Нам хочется, чтобы после обучения нейроны внутри сетки были максимально разнообразными. Для этого веса лучше инициализировать случайно. В будущем мы обсудим грамотные способы инициализации, которые не портят обучение.