9. Универсальный регрессор#
Маша доказала Паше, что у неё всё в полном порядке с логикой. Теперь она собирается доказать ему, что с помощью нейронной сетки можно приблизить любую непрерывную функцию от одного аргумента \(f(x)\) со сколь угодно большой точностью[1].
Подсказка
Вспомните, что любую непрерывную функцию можно приблизить с помощью кусочно-линейной функции (ступеньки). Осознайте как с помощью пары нейронов можно описать такую ступеньку. Соедините все ступеньки в сумму с помощью выходного нейрона.
Решение
Не нужно воспринимать эту задачку как строгое доказательство. Скорее, это «показательство». Мы хотим приблизить функцию \(f(x)\) с какой-то точностью. Будем делать это с помощью кусочно-линейных ступенек. Чем выше точность, тем больше будем рисовать ступенек[2].
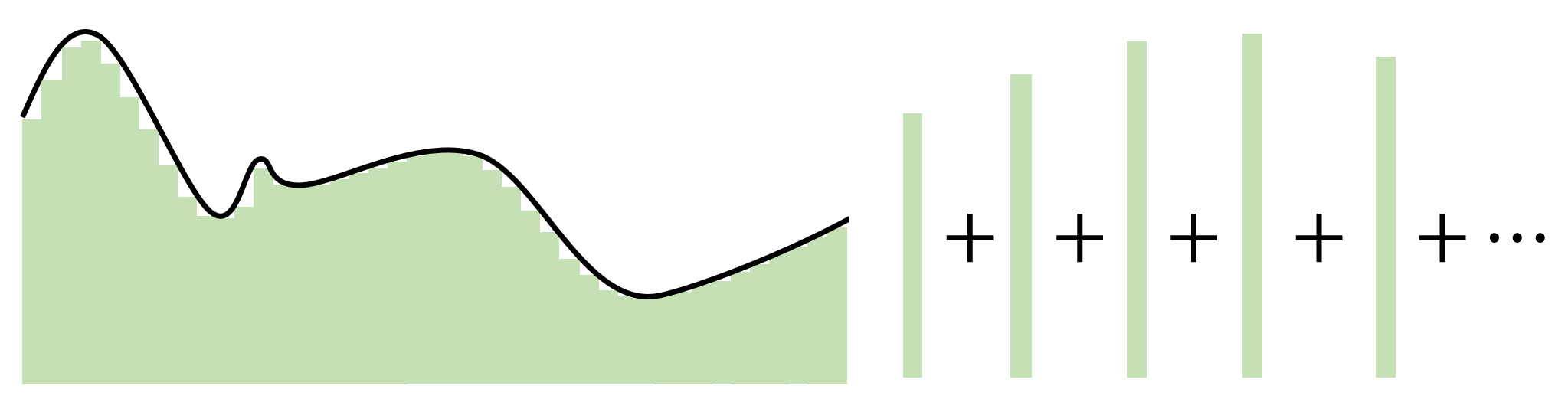
Высоту ступеньки определяют по-разному. Чаще всего, как значение функции в середине выбранного отрезка, \(b_i = f(\frac{a_i + a_{i+1}}{2})\). Тогда всю функцию целиком можно приблизить суммой
Давайте попробуем описать с помощью нейрона одну из ступенек. Пусть высота этой ступеньки равна \(b_i\). Шагать по оси \(x\) мы будем с фиксированным шагом \(h\), поэтому \(a_{i+1} = a_i + h\).
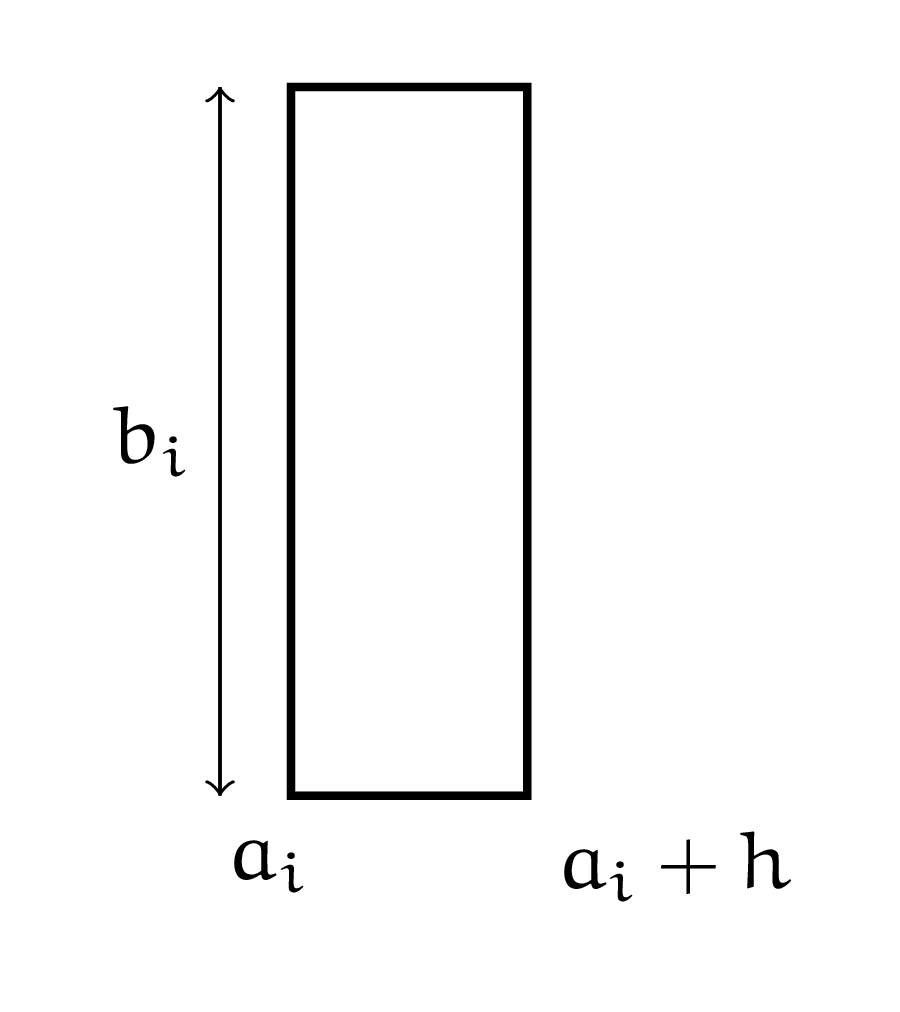
Если \(x\), для которого мы ищем \(f(x)\), попадает в полуинтервал, на котором задана наша ступенька, мы будем приближать \(f(x)\) этой ступенькой. Ступенька состоит из двух линий. Выходит, что она будет описываться двумя нейронами. Если мы внутри ступеньки, значит \(a_i \le x < a_i + h\). Пара нейронов должна сравнить \(x\) с \(a_i\) и \(a_i + h\). Можно записать попадание \(x\) в ступеньку следующим образом:
Если оба условия — неправда, получаем \(1\). Мы в ступеньке. Если хотя бы одно из них выполнено — мы вылетаем за ступеньку. Одновременно оба условия никогда не выполняются. Нарисуем это в виде сетки. В качестве функции активации используем единичную ступеньку.
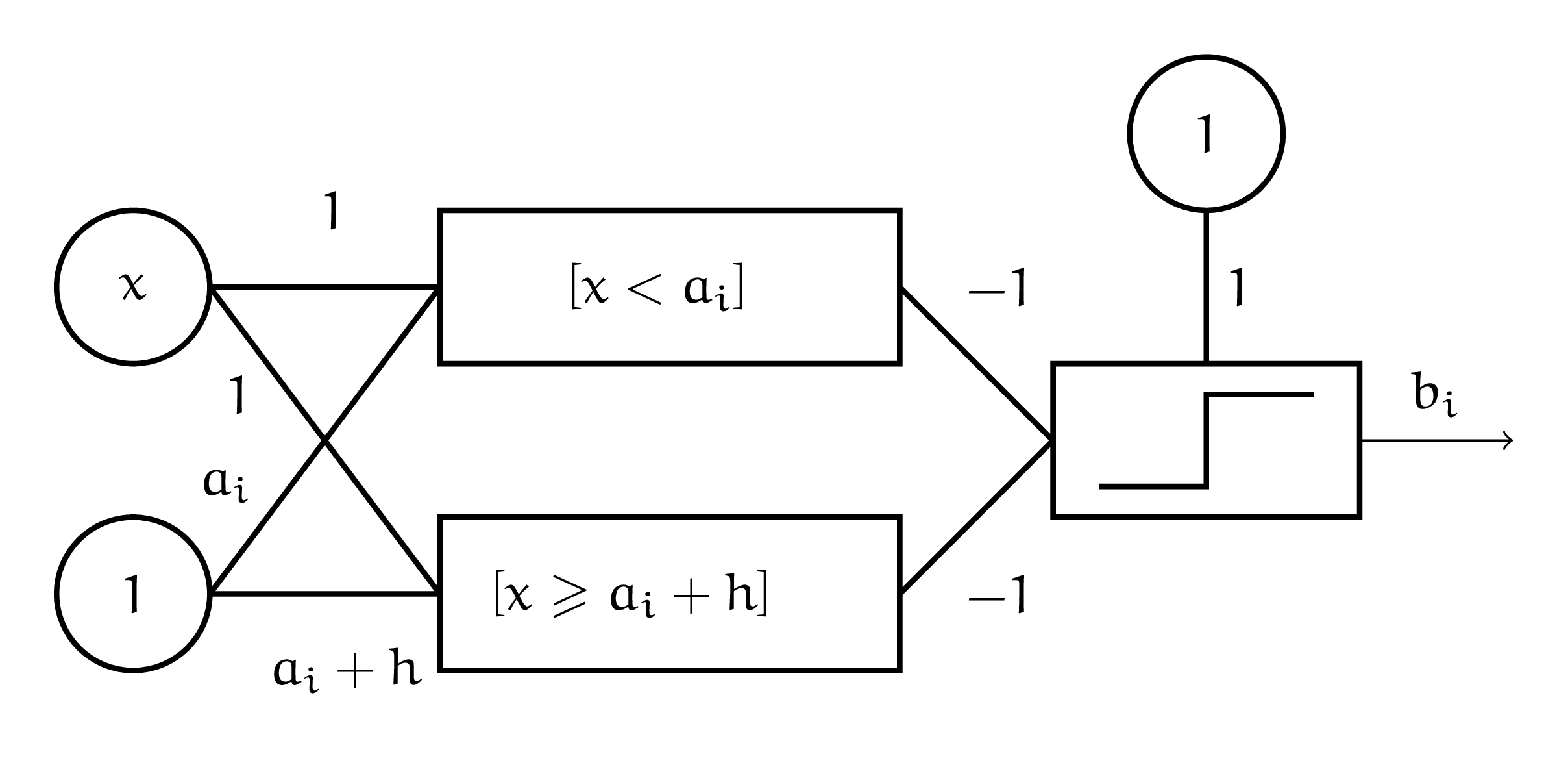
Нарисуем такую сетку для каждой ступеньки. Если мы попали в ступеньку, сетка будет выплёвывать со второго слоя единичку. Там мы будем умножать её на \(b_i\) и посылать на внешний слой.
Мы всегда будем попадать только в одну из ступенек, значит только один из слоёв выдаст нам \(1\). Все остальные выдадут \(0\). На внешнем слое нам остаётся только просуммировать всё, что к нам пришло и выдать ответ.
Чем больше ступенек мы добавляем в модель, тем точнее наша апроксимация. Можно немного поколдовать с получившейся архитектурой и удалить из неё части, которые друг-друга дублируют.
Про регрессор понятно. А почему неросеть может решить любую задачу классификации? Сможете придумать «показательство»?
