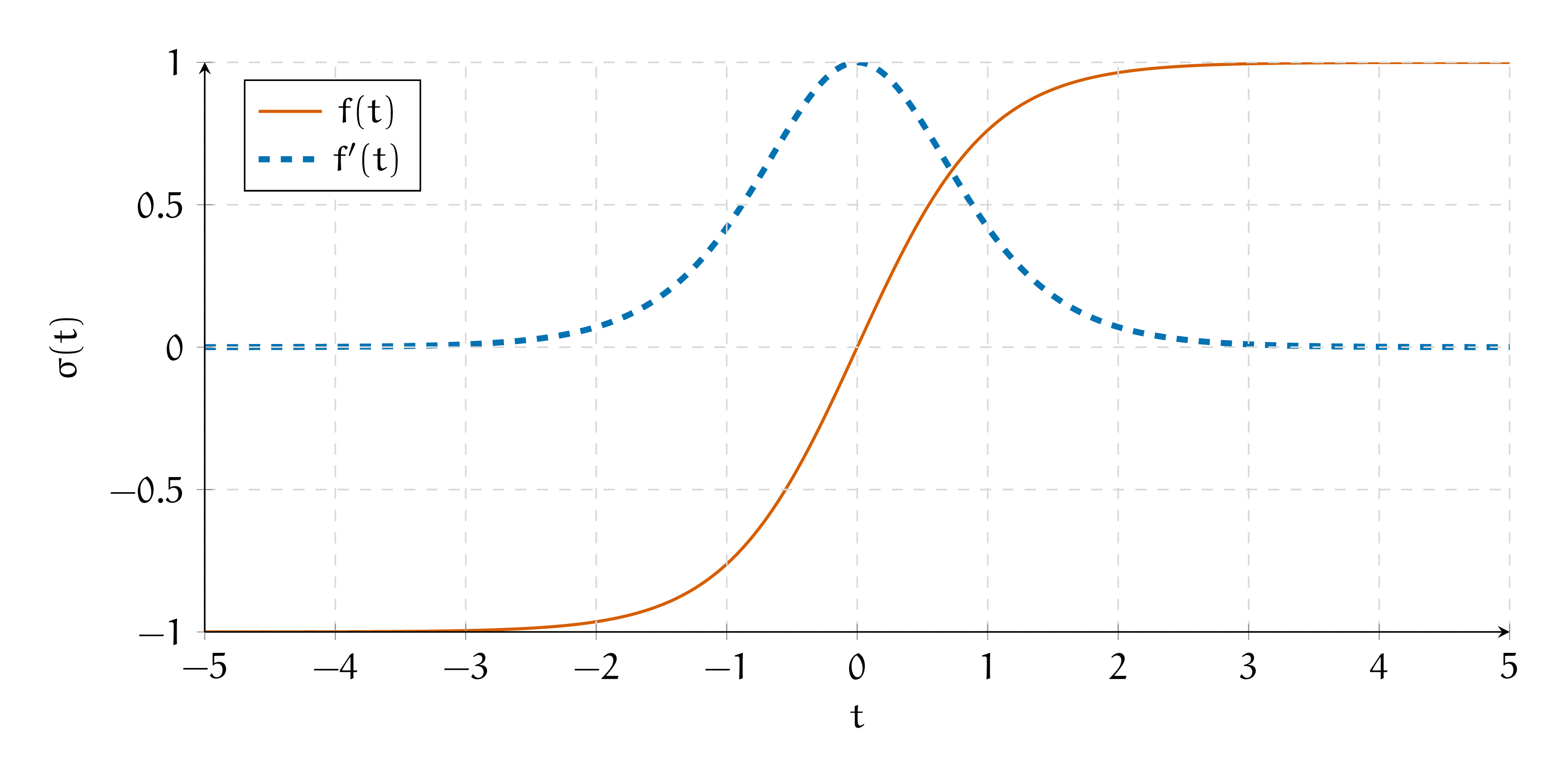4. Гиперболический тангенс#
Функция \(f(t) = \tanh(t) = \frac{2}{1 + e^{-2t}} - 1\) называется гиперболическим тангенсом.
а) Что происходит при \(t \to +\infty\)? А при \(t \to -\infty\)?
Решение
Мы знаем, что при \(t \to +\infty\) функция \(e^{-2t} \to 0\), значит \(f(t) \to 1.\)
По аналогии при \(t \to -\infty\) функция \(e^{-2t} \to \infty\), значит \(f(t) \to -1.\)
б) Как связаны между собой \(f(t)\) и \(f'(t)\)? Как они выглядят на графике?
Решение
Если взять производную сложной функции, можно получить, что
Изобразим функцию активации и её производную на графике
в) Выпишите формулы для forward pass и backward pass через слой с тангенсом.
Решение
Мы уже нашли выше производную. У гиперболического тангенса нет обучаемых параметров, получается прямой проход через неё делается по формуле
Обратный шаг делается по формуле
То же самое можно записать как
г) Правда ли, что тангенс способствует затуханию градиента и параличу нейронной сети? Какое максимальное значение принимает производная тангенса?
Решение
Да, правда. Значение 1 - \(f(t)^2\) лежит между \(0\) и \(1\).
д) Как у тангенса дела с центированием относительно нуля?
Решение
В отличие от сигмоиды, тангенс центрирован относительно нуля. Пожалуй, это его единственный плюс. В остальном, это плохая функция активации, способствующая затуханию градиента.
е) Сигмоиду обычно используют для того, чтобы на последнем слое получать вероятности. Либо в местах, где внутри нейросети нужно отщипнуть долю от какого-нибудь числа (например, в LSTM). Как думаете, где на практике используют тангенс?
Решение
Тангенс не используют в качестве функции активации из-за тех же самых недостатков, что и сигмоиду. Обычно его используют, когда на выходе из слоя нужно получить число с отрезка \([-1; 1]\).
Например, когда работают с картинками, их нормируют на отрезок \([-1; 1].\) Если мы захотим обучить нейросетку, которая генерирует картинки, на выходе нам надо будет получать числа с этого отрезка. Тут нам и пригодится тангенс.